La¬†Calorina √©s una √†rea de la¬†matem√†tica aplicada que utilitza¬†models per estudiar interaccions en estructures formalitzades d'incentius (els anomenats ¬ęjocs¬Ľ). La teoria de jocs s' ha convertit en una eina summament important per a la teoria econ√≤mica i ha contribu√Įt a comprendre m√©s adequadament la conducta humana enfront de la presa de decisions. Els seus investigadors estudien les¬†estrat√®gies √≤ptimes, aix√≠ com el comportament previst i observat d'individus en jocs. Tipus d' interacci√≥ aparentment diferents poden presentar en realitat una estructura d' incentiu similar i, per tant, es pot representar mil vegades conjuntament un mateix joc.1‚Äč
Desenvolupada en els seus comen√ßaments com una eina per entendre el comportament de l' economia, la teoria de jocs s' usa actualment en molts camps, com en la¬†biologia, sociologia,¬†politologia,¬†psicologia,¬†filosofia i¬†ci√®ncies de la computaci√≥.¬†Va experimentar un creixement substancial i es va formalitzar per primera vegada a partir dels treballs de¬†John von Neumann i¬†Oskar Morgenstern, abans i durant la¬†Guerra Freda, degut sobretot a la seva aplicaci√≥ a l'estrat√®gia¬†militar, en particular a causa del concepte¬†de destrucci√≥ m√ļtua garantida . Des dels setanta, la teoria de jocs s' ha aplicat a la conducta animal, incloent-hi el desenvolupament de les esp√®cies per la selecci√≥ natural. Arran de jocs com el¬†dilema del presoner, en els quals l'egoisme generalitzat perjudica els jugadors, la teoria de jocs ha atret tamb√© l'atenci√≥ dels investigadors en¬†inform√†tica, usant-se en¬†intel¬∑lig√®ncia artificial i¬†cibern√®tica.
Els conflictes entre √©ssers racionals que recelen l' un de l' altre, o la pugna entre competidors que interactuen i s' influeixen m√ļtuament, que pensen i que, fins i tot, poden ser capa√ßos de trair-se l' un a l' altre, constitueixen el camp d' estudi de la teoria de jocs, la qual es basa en una an√†lisi matem√†tica rigorosa per√≤ que, tanmateix, sorgeix de manera natural en observar i analitzar un conflicte des d' un punt de vista racional. Des de l'enfocament d'aquesta teoria, un ¬ęjoc¬Ľ √©s una situaci√≥ conflictiva en la qual priman interessos contraposats d'individus o institucions, i en aquest context una part, en prendre una decisi√≥, influeix sobre la decisi√≥ que prendr√† l'altra; aix√≠, el resultat del conflicte es determina a partir de totes les decisions preses per tots els actuants.
La teoria de jocs planteja que hi ha d'haver una forma racional de jugar a qualsevol ¬ęjoc¬Ľ (o de negociar en un conflicte), especialment en el cas d'haver-hi moltes situacions enganyoses i segones intencions; aix√≠, per exemple, l'anticipaci√≥ m√ļtua de les intencions del contrari, que succeeix en jocs com l'escac o el p√≤quer, dona lloc a cadenes de raonament te√≤ricament infinites, les quals poden tamb√© traslladar-se a l'√†mbit de resoluci√≥ de conflictes reals i complexos. En s√≠ntesi, i tal com es va comentar, els individus, en interactuar en un conflicte, obtindran resultats que d' alguna manera s√≥n totalment dependents de tal interacci√≥.2‚Äč
Aix√≠, des que Von Neumann, Morgenstern i¬†John Nash van delinear els postulats b√†sics d'aquesta teoria durant les d√®cades del 40 i 50, diverses han estat les aplicacions que se li han atorgat a aquesta eina en el camp de les decisions econ√≤miques, arribant fins i tot a modificar la manera en qu√® els economistes interpretaven la presa de decisions i la consecuci√≥ del benestar com√ļ.
Representació de jocs
El dilema del presoner
Un dels problemes que planteja l'equilibri de Nash es troba en qu√® no condueix necess√†riament a situacions eficients en el sentit de Pareto1. L'an√†lisi original d'aquest joc es basa en una situaci√≥ en la qual s'interroga en habitacions diferents a dues persones que han com√®s conjuntament un robatori armat a un banc; tot i aix√≤, els diners sostrets no es troben a les seves mans i, per aix√≤, la policia nom√©s pot inculpar-los per tinen√ßa il¬∑l√≠cita d'armes, en mancar d'altres proves. Aix√≠, en ser interrogats per separat, cadascun d'ells tindria la possibilitat de confessar-se culpable, implicar l'altre presoner o negar haver participat en l'atracament. Tanmateix, la policia els pot proposar un tracte i, a trav√©s de l' √ļs d' un adequat esquema d' incentius, fer que ambd√≥s confi√Įn la participaci√≥ en el fet, aconseguir que la veritat surti a la llum i condemnar-los. A continuaci√≥ es veur√† que una adequada proposta efectuada pel cos de policies, pot conduir al fet que la racionalitat i l' egoisme individual amb qu√® solen ser preses les decisions es pot tornar en contra de l' inter√®s conjunt d' aquests subjectes, compatibles amb les idees d' Adam Smith. Per demostrar aix√≤, consid&;reas per exemple, el joc anomenat¬†El dilema del presoner. Aquest joc permet comprendre que mantenir la cooperaci√≥ √©s quelcom summament dif√≠cil. Moltes vegades els individus no cooperen (aquest cas √©s un exemple parad√≤gic, ja que demostra els beneficis que s'obtindrien en mantenir la cooperaci√≥ entre qualsevol grup d'individus, per√≤ alhora demostra que aix√≤, sota certs postulats, √©s impossible d'aconseguir), i les seves decisions individuals no necess√†riament condueixen al mutu benestar.
Forma normal d' un joc
Un joc de forma normal
|
El jugador 2 elegeix esquerra | El jugador 2 elegeix dreta |
| El jugador 1 elegeix a dalt |
4, 3 |
-1, -1 |
| El jugador 1 elegeix avall |
0, 0 |
3, 4 |
La forma normal (o forma estrat√®gica) d'un joc √©s una¬†matriu de pagaments, que mostra els jugadors, les estrat√®gies i les recompenses (vegeu l'exemple a la dreta). Hi ha dos tipus de jugadors; un elegeix la fila i un altre la columna. Cada jugador t√© dues estrat√®gies, que estan especificades pel nombre de files i el nombre de columnes. Les recompenses s' especifiquen a l' interior. El primer n√ļmero √©s la recompensa rebuda pel jugador de les files (el¬†Jugador 1 en el nostre exemple); el segon √©s la recompensa del jugador de les columnes (el¬†Jugador 2 en el nostre exemple). Si el¬†jugador 1 elegeix a dalt i el¬†jugador 2 elegeix esquerra llavors les seves recompenses s√≥n 4 i 3, respectivament.
Quan un joc es presenta de forma normal, es pressuposa que tots els jugadors actuen simultàniament o, almenys, sense saber l' elecció que pren l' altre. Si els jugadors tenen alguna informació sobre les eleccions d' altres jugadors el joc es presenta habitualment en la forma extensiva.
Tamb√© existeix una forma normal redu√Įda. Aquesta combina estrat√®gies associades amb el mateix pagament.
Forma extensiva d' un joc

Un joc de forma extensiva.
La representaci√≥ de jocs en forma extensiva modela jocs amb algun ordre que s' ha de considerar. Els jocs es presenten com¬†a arbres (com es mostra a la dreta). Cada¬†v√®rtex o¬†node representa un punt on el jugador pren decisions. El jugador s' espec√≠fica per un n√ļmero situat al costat del v√®rtex. Les l√≠nies que parteixen del v√®rtex representen accions possibles per al jugador. Les recompenses s' especifiquen a les fulles de l' arbre.
En el joc que es mostra en l'exemple hi ha dos jugadors. El jugador 1 mou primer i elegeix F o U. El jugador 2 veu el moviment del jugador 1 i elegeix A o R. Si el jugador 1 elegeix U i llavors el jugador 2 elegeix A, llavors el jugador 1 n' obté 8 i el jugador 2 n' obté 2.
Els jocs en forma extensiva poden modelar també jocs de moviments simultanis. En aquests casos es dibuixa una línia puntejada o un cercle al voltant de dos vèrtexs diferents per representar-los com a part del mateix conjunt d'informació (per exemple, quan els jugadors no saben en quin punt es troben).
La forma normal dona al matem√†tic una notaci√≥ senzilla per a l'estudi dels problemes d'equilibri, perqu√® desestima la q√ľesti√≥ de com les estrat√®gies s√≥n calculades o, en altres paraules, de com el joc √©s jugat en realitat. La notaci√≥ convenient per tractar aquestes q√ľestions, m√©s rellevants per a la¬†teoria combinat√≤ria de jocs, √©s la forma extensiva del joc.
Tipus de jocs i exemples
La teoria classifica els jocs en moltes categories que determinen quins mètodes particulars es poden aplicar per resoldre'ls (i, de fet, també com es defineix "resolució" en una categoria particular). Les categories comunes inclouen:
Jocs simètrics i asimètrics
Un joc asimètric
|
E | F |
| E |
1, 2 |
0, 0 |
| F |
0, 0 |
1, 2 |
Un joc sim√®tric √©s un joc en el qual les recompenses per jugar una estrat√®gia en particular depenen nom√©s de les estrat√®gies que emprin els altres jugadors i no de qui les jugui. Si les identitats dels jugadors es poden canviar sense que canvi√Įn les recompenses de les estrat√®gies, llavors el joc √©s sim√®tric. Molts dels jocs 2√ó2 m√©s estudiats s√≥n sim√®trics. Les representacions est√†ndard del¬†joc del gallina, el¬†dilema del presoner i la¬†ca√ßa del c√©rvol s√≥n jocs sim√®trics.3‚Äč
Els jocs asimètrics més estudiats són els jocs on no hi ha conjunts d' estratègies idèntiques per a ambdós jugadors. Per exemple, el joc de l'ultimàtum i el joc del dictador tenen diferents estratègies per a cada jugador; no obstant això, hi pot haver jocs asimètrics amb estratègies idèntiques per a cada jugador. Per exemple, el joc mostrat a la dreta és asimètric malgrat tenir conjunts d'estratègies idèntics per a ambdós jugadors.
Jocs de suma zero i de suma diferent de zero
Un joc de suma zero
|
A | B | C |
| 1 |
30, -30 |
-10, 10 |
20, -20 |
| 2 |
10, -10 |
20, -20 |
-30, 30 |
En els jocs de suma zero el benefici total per a tots els jugadors del joc, en cada combinació d'estratègies, sempre suma zero (en altres paraules, un jugador es beneficia només a expenses d'altres). El go, l'escac, el pòker i el joc de l'ós són exemples de jocs de suma zero, perquè es guanya exactament la quantitat que perd l'oponent. Com a curiositat, el futbol va deixar fa uns anys de ser de suma zero, ja que les victòries reportaven 2 punts i l'empat 1 (considérese que ambdós equips parteixen inicialment amb 1 punt), mentre que en l'actualitat les victòries reporten 3 punts i l'empat 1.
La majoria dels exemples reals en negocis i pol√≠tica, igual que el¬†dilema del presoner, s√≥n jocs de summa diferent de zero, perqu√® alguns desenlla√ßos tenen resultats nets majors o menors que zero. √Čs a dir, el guany d' un jugador no necess√†riament es correspon amb la p√®rdua d' un altre. Per exemple, un contracte de negocis involucra idealment un desenlla√ß de suma positiva, on cada oponent acaba en una posici√≥ millor que la que tindria si no s'hagu√©s donat la negociaci√≥.
Es pot analitzar més fàcilment un joc de suma diferent de zero, i qualsevol joc es pot transformar en un joc de suma zero afegint un jugador "fictici" addicional ("el tauler" o "la banca"), les pèrdues del qual compensin els guanys nets dels jugadors.
La matriu de pagaments d' un joc és una forma convenient de representació. Per exemple, un joc de suma zero de dos jugadors amb la matriu que es mostra a la dreta.
Criteris ¬ęmaximin¬Ľ i ¬ęminimax¬Ľ
Els criteris ¬ęmaximin¬Ľ i ¬ęminimax¬Ľ estableixen que cada jugador ha de minimitzar la seva p√®rdua m√†xima:
- Criteri ¬ęmaximin¬Ľ: el jugador A, elegeix que el seu cobrament m√≠nim possible sigui el m√©s gran.
- Criteri ¬ęminimax¬Ľ: el jugador B elegeix que el pagament m√†xim a A sigui el menor possible.
Equilibri de Nash
Els equilibris de les estrat√®gies dominants estan molt b√© quan apareixen en els jocs, per√≤ desafortunadament, aix√≤ no ocorre amb freq√ľ√®ncia.
Un parell d' estratègies és un equilibri de Nash si l' elecció del jugador A és òptima, donada elecció de B, i la de B és òptima, atesa la d' A.
L'equilibri de Nash pot interpretar-se com un parell d'expectatives sobre l'elecció de cada persona tal que, quan l'altra revela la seva elecció, cap de les dues vol canviar de conducta.
Cada jugador coneix i ha adoptat la seva millor estrat√®gia, i tots coneixen les estrat√®gies dels altres. Conseq√ľentment, cada jugador individual no guanya res modificant la seva estrat√®gia mentre els altres mantinguin les seves. Aix√≠, cada jugador est√† executant el millor "moviment" que pot donats els moviments dels altres jugadors.
Jocs cooperatius
Un joc cooperatiu es caracteritza per un contracte que es pot fer complir. La teoria dels jocs cooperatius dona justificacions de contractes plausibles. La plausibilitat d'un contracte està molt relacionada amb l'estabilitat.
Dos jugadors negocien tant volen invertir en un contracte. La teoria de la negociació axiomàtica ens mostra quanta inversió és convenient per a nosaltres. Per exemple, la solució de Nash per a la negociació demanda que la inversió sigui justa i eficient.
De qualsevol manera, podríem no estar interessats en la justícia i exigir més. De fet, hi ha un joc no cooperatiu creat per Ariel Rubinstein consistent a alternar ofertes, que recolza la solució de Nash considerant-la la millor, mitjançant l'anomenat equilibri de Nash. El joc cooperatiu a l'hora de Matemàtica
En aquest sentit, proposem analitzar seq√ľ√®ncies did√†ctiques perqu√® els nostres alumnes "facin matem√†tica", √©s a dir, exploren, estableixin relacions, confrontin les seves produccions amb les d'altres, discuteixin amb els seus parells, prenguin decisions, argumentin, validesa proposicions, en produeixin coneixement. Perqu√® aquesta feina sigui possible, cal plantejar problemes que impliquin un cert nivell de desafiament; un context f√®rtil per al planter d'aquests desafiaments √©s el dels jocs.
Simultanis i seq√ľencials
Els jocs simultanis s√≥n jocs en els quals els jugadors mouen simult√†niament o en els quals aquests desconeixen els moviments anteriors d' altres jugadors. Els jocs seq√ľencials (o din√†mics) s√≥n jocs en els quals els jugadors posteriors tenen algun coneixement de les accions pr√®vies. Aquest coneixement no necess√†riament ha de ser perfecte; nom√©s ha de consistir en quelcom d' informaci√≥. Per exemple, un jugador pot con√®ixer que un jugador no va realitzar una acci√≥ determinada, per√≤ no saber quina de les altres accions disponibles va triar.
La difer√®ncia entre jocs simultanis i seq√ľencials es recull en les representacions discutides pr√®viament. La forma normal s' usa per representar jocs simultanis, i l' extensiva per representar jocs seq√ľencials.
Jocs d' informació perfecta

Un joc d'informació imperfecta (les línies puntejades representen la ignorància de la part del jugador 2).
Un subconjunt important dels jocs seq√ľencials √©s el conjunt dels jocs d' informaci√≥ perfecta. Un joc √©s d'informaci√≥ perfecta si tots els jugadors coneixen els moviments que han efectuat pr√®viament tots els altres jugadors; aix√≠ que nom√©s els jocs seq√ľencials poden ser jocs d'informaci√≥ perfecta, ja que en els jocs simultanis no tots els jugadors (sovint cap) coneixen les accions de la resta. La majoria dels jocs estudiats en la teoria de jocs s√≥n jocs d'informaci√≥ imperfecta, tot i que alguns jocs interessants s√≥n d'informaci√≥ perfecta, incloent-hi el joc de l'ultim√†tum i el¬†joc del cigne. Tamb√© molts jocs populars s√≥n d'informaci√≥ perfecta, incloent-hi¬†l'escac i el¬†go.
La informació perfecta es confon sovint amb la informació completa, que és un concepte similar. La informació completa requereix que cada jugador conegui les estratègies i recompenses de la resta però no necessàriament les accions.
En els jocs d'informació completa cada jugador té la mateixa "informació rellevant al joc" que els altres jugadors. L' escacs i el dilema del presoner exemplifiquen jocs d' informació completa. Els jocs d'informació completa ocorren rarament en el món real, i els teòrics dels jocs, usualment els veuen només com aproximacions al joc realment jugat.
El matemàtic anglès, i catedràtic emèrit de la Universitat de Princeton, John Conway, va desenvolupar una notació per a alguns jocs d'informació completa i va definir diverses operacions en aquests jocs, originalment per estudiar els finals de go, tot i que bona part d'aquesta anàlisi es va enfocar en nim. Això va devèn en la teoria de jocs combinatòria.
Conway va descobrir que existeix una subclisi d'aquells jocs que poden ser usats com a n√ļmeros, com va descriure en el seu llibre¬†On Numbers and Games (1976), arribant a la classe molt general dels¬†n√ļmeros surreals.
Jocs de longitud infinita
Per raons òbvies, els jocs estudiats pels economistes i els jocs del món real finalitzen generalment després d'un nombre finit de moviments. Els jocs matemàtics purs no tenen aquestes restriccions i la teoria de conjunts estudia jocs d'infinits moviments, on el guanyador no es coneix fins que tots els moviments es coneguin.
L'inter√®s en aquesta situaci√≥ no sol ser decidir quina √©s la millor manera de jugar a un joc, sin√≥ simplement quin jugador t√© una estrat√®gia guanyadora (Es pot provar, usant¬†l'axioma d'elecci√≥, que hi ha jocs ‚ÄĒfins i tot d'informaci√≥ perfecta, i on les √ļniques recompenses s√≥n "perdre" i "guanyar"‚ÄĒ per als quals¬†cap jugador t√© una estrat√®gia guanyadora.) L' exist√®ncia d' aquestes estrat√®gies t√© conseq√ľ√®ncies importants en la¬†teoria descriptiva de conjunts.
Jocs combinatoris
Els jocs en què la dificultat de trobar una estratègia òptima prové de la multiplicitat de moviments possibles s' anomenen jocs combinatoris. Alguns exemples d'aquests jocs poden ser escacs i go. Els jocs que impliquen informació imperfecta o incompleta també poden tenir un fort caràcter combinatori, per exemple el backgammon. No hi ha una teoria unificada que s' ocupa dels elements combinatoris en els jocs. Hi ha, però, eines matemàtiques que poden resoldre problemes particulars i respondre a preguntes generals.
S'han estudiat jocs¬†d'informaci√≥ perfecta en la teoria combinat√≤ria de jocs, que ha desenvolupat noves representacions, com per exemple els¬†n√ļmeros surreals, aix√≠ com m√®todes de prova combinatoris i algebraics (i de vegades no constructius) per¬†resoldre jocs de certs tipus, incloent jocs "loopy" que poden donar lloc a seq√ľ√®ncies de moviments infinitament llargues. Aquests m√®todes es dirigeixen a jocs amb major complexitat combinat√≤ria que els normalment considerats en la teoria de jocs tradicional (o "econ√≤mica"). Un joc t√≠pic que s'ha resolt d'aquesta manera √©s hexadecimal. Un camp relacionat d' estudi, basat en la¬†teoria de la complexitat computacional, √©s la complexitat del joc, que s' ocupa d' estimar la dificultat computacional de trobar estrat√®gies √≤ptimes.
La investigaci√≥ en¬†intel¬∑lig√®ncia artificial ha abordat jocs d'informaci√≥ perfectes i imperfectes (o incomplets) que tenen estructures combinat√≤ries molt complexes (com escacs, go o backgammon) per als quals no s'han trobat estrat√®gies √≤ptimes comprovables. Les solucions pr√†ctiques impliquen l' heur√≠stica computacional, com la¬†poda alfa-beta o l' √ļs de¬†xarxes neuronals artificials entrenades per l' aprenentatge de refor√ß, que fan que els jocs siguin m√©s manejables en la pr√†ctica de la computaci√≥.
Jocs discrets i continus
Gran part de la teoria de jocs es refereix a jocs finits i discrets, que tenen un nombre finit de jugadors, moviments, esdeveniments, resultats, etc. Tanmateix, molts conceptes es poden estendre. Els jocs continus permeten als jugadors elegir una estratègia a partir d' un conjunt d' estratègies contínues. Per exemple, la competició de Cournot es modela típicament amb les estratègies dels jugadors qualssevol quantitats no negatives, incloent quantitats fraccionàries.
Jocs diferencials
Els jocs diferencials com el joc de recerca contínua i evasió són jocs continus on l' evolució de les variables d' estat dels jugadors es regeix per equacions diferencials. El problema de trobar una estratègia òptima en un joc diferencial està estretament relacionat amb la teoria del control òptim. En particular, existeixen dos tipus d'estratègies: les estratègies de bucle obert utilitzen el principi de Pontryagin màxim, mentre que les estratègies de bucle tancat utilitzen el mètode de programació dinàmica de Bellman.
Un cas particular de jocs diferencials són els jocs amb un horitzó temporal aleatori. En aquests jocs, el temps terminal és una variable aleatòria amb una funció de distribució de probabilitat donada. Per tant, els jugadors maximitzar l' expectativa matemàtica de la funció de cost. Es va demostrar que el problema d'optimització modificat es pot reformular com un joc diferencial amb descompte en un interval de temps infinit.
Jocs de molts jugadors i poblacions
Els jocs amb un n√ļmero arbitrari, per√≤ finit, de jugadors sovint s'anomenen jocs de la n-persona. La teoria evolutiva dels jocs considera els jocs que involucren una poblaci√≥ de prenedors de decisions, on la freq√ľ√®ncia amb la qual es pren una decisi√≥ particular pot canviar amb el temps en resposta a les decisions preses per tots els individus de la poblaci√≥. En biologia, aix√≤ s'utilitza per modelar l'evoluci√≥ (biol√≤gica), on els organismes programats gen√®ticament passen al llarg quelcom de la seva programaci√≥ de l'estrat√®gia a la seva descend√®ncia. En economia, la mateixa teoria est√† destinada a captar els canvis de poblaci√≥ perqu√® les persones juguen el joc moltes vegades dins de la seva vida, i conscientment (i potser racionalment) canviar les estrat√®gies.
Resultats estocàstics (i relació amb altres camps)
Els problemes individuals de decisió amb resultats estocàstics de vegades es consideren "jocs d'un sol jugador". Aquestes situacions no es consideren teòriques de joc per part d' alguns autors. Poden ser modelades utilitzant eines similars dins de les disciplines relacionades de la teoria de la decisió, la investigació d'operacions i àrees d'intel·ligència artificial, particularment, la planificació d'IA (amb incertesa) i sistemes multi-agents. Tot i que aquests camps poden tenir motivadors diferents, les matemàtiques implicades són substancialment les mateixes, per exemple, usant processos de decisió de Markov (MDP). Els resultats estocàstics també poden ser modelats en termes de la teoria de jocs agregant un jugador d'acció aleatòria que fa "moviments de la casualitat" ("moviments per naturalesa"). Aquest jugador no sol ser considerat un tercer jugador en el que altrament és un joc de dos jugadors, sinó que simplement serveix per proporcionar un rol de donat quan sigui requerit pel joc.
Per a alguns problemes, els diferents enfocaments per modelar resultats estoc√†stics poden conduir a solucions diferents. Per exemple, la difer√®ncia en l'enfocament entre MDPs i la soluci√≥¬†minimax √©s que aquest √ļltim considera el pitjor cas sobre un conjunt de moviments adversaris, en lloc de raonar en l'expectativa sobre aquests moviments donats una distribuci√≥ de probabilitat fixa. L'enfocament minimax pot ser avantatj√≥s quan no es disposa de models estoc√†stics d'incertesa, per√≤ tamb√© pot estar sobreestimant esdeveniments extremadament improbables (per√≤ costosos), canviant dram√†ticament l'estrat√®gia en aquests escenaris si se suposa que un adversari pot for√ßar que succeeixi tal esdeveniment. Tamb√© s'han estudiat models generals que inclouen tots els elements de resultats estoc√†stics, adversaris i observabilitat parcial o sorollosa (de moviments d'altres jugadors). Es considera que el "patr√≥ or" √©s un joc estoc√†stic parcialment observable (POSG), per√≤ pocs problemes realistes s√≥n computacionalment factibles en la representaci√≥ POSG.
Metagames
Aquests són jocs en els quals es tracta de desenvolupar les regles per a un altre joc, l' objectiu o el jugador. Els metagames busquen maximitzar el valor d'utilitat del conjunt de regles desenvolupat. La teoria dels metagames està relacionada amb la teoria del disseny de mecanismes.
El terme anàlisi metagame també s'utilitza per referir-se a un enfocament pràctic desenvolupat per Nigel Howard. Per la qual cosa una situació s' emmarca com un joc estratègic en el qual les parts interessades tracten de realitzar els seus objectius per mitjà de les opcions disponibles. Els esdeveniments posteriors han portat a la formulació de l' anàlisi de la confrontació.
Aplicacions
La teoria de jocs té la característica de ser una àrea en què la substància subjacent és principalment una categoria de matemàtiques aplicades, però la majoria de la recerca fonamental és exercida per especialistes en altres àrees. En algunes universitats s'ensenya i s'investiga gairebé exclusivament fora del departament de matemàtica.
Aquesta teoria té aplicacions en nombroses àrees, entre les quals cal destacar les ciències econòmiques, la biologia evolutiva, la psicologia, les ciències polítiques, el disseny industrial, la investigació operativa, la informàtica i l' estratègia militar.
Economia i negocis
Els economistes han usat la teoria de jocs per analitzar un ampli ventall de problemes econòmics, incloent subhastes, duopolis, oligopolis, la formació de xarxes socials, i sistemes de votacions. Aquestes investigacions normalment estan enfocades a conjunts particulars d' estratègies coneguts com a conceptes de solució. Aquests conceptes de solució estan basats normalment en el requerit per les normes de racionalitat perfecta. El més famós és l'equilibri de Nash. Un conjunt d'estratègies és un equilibri de Nash si cadascuna representa la millor resposta a altres estratègies. D'aquesta forma, si tots els jugadors estan aplicant les estratègies en un equilibri de Nash, no tenen cap incentiu per canviar de conducta, ja que la seva estratègia és la millor que poden aplicar donades les estratègies dels altres.
Les recompenses dels jocs normalment representen la utilitat dels jugadors individuals. Sovint les recompenses representen diners, que es presumeix corresponen a la utilitat d'un individu. Aquesta presumpció, però, pot no ser correcta.
Un document de teoria de jocs en economia comença presentant un joc que és una abstracció d'una situació econòmica particular. S' elegeixen una o més solucions, i l' autor demostra quin conjunt d' estratègies corresponen a l' equilibri en el joc presentat. Els economistes i professors d'escoles de negocis suggereixen dos usos principals.
Descriptiva

Un joc del cigne de tres fases.
L' √ļs principal √©s informar sobre el comportament de les poblacions humanes actuals. Alguns investigadors creuen que trobar l'equilibri dels jocs pot predir com es comportarien les poblacions humanes si s'enfrontessin a situacions an√†logues al joc estudiat. Aquesta visi√≥ particular de la teoria de jocs s' ha criticat en l' actualitat. En primer lloc, se la cr√≠tica perqu√® els sup√≤sits dels te√≤rics es violen freq√ľentment. Els te√≤rics de jocs poden suposar jugadors que es comporten sempre racionalment i actuen per maximitzar els seus beneficis (el model¬†Homo oeconomicus), per√≤ els humans reals sovint actuen irracionalment o racionalment per√≤ buscant el benefici d'un grup m√©s gran (altruisme).
Els te√≤rics de jocs responen comparant els seus sup√≤sits amb els quals s' empren en f√≠sica. Aix√≠, tot i que els seus sup√≤sits no es mantenen sempre, poden tractar la teoria de jocs com una¬†idealitzaci√≥ raonable, de la mateixa manera que els models usats pels¬†f√≠sics. Tanmateix, aquest √ļs de la teoria de jocs s' ha seguit criticant perqu√® alguns experiments han demostrat que els individus no es comporten segons estrat√®gies d' equilibri. Per exemple, en el joc del cigne, el joc d'endivinar 2/3 de la mitjana i el joc del dictador, les persones sovint no es comporten segons l'equilibri de Nash. Aquesta controv√®rsia s' est√† resolent actualment.4‚Äč
D' altra banda, alguns autors addueixen que els equilibris de Nash no proporcionen prediccions per a les poblacions humanes, sin√≥ que proporcionen una explicaci√≥ de per qu√® les poblacions que es comporten segons l' equilibri de Nash romanen en aquesta conducta. Tanmateix, la q√ľesti√≥ sobre quanta gent es comporta aix√≠ roman oberta.
Alguns teòrics de jocs han posat esperances en la teoria evolutiva de jocs per resoldre aquestes preocupacions. Aquests models pressuposen o no racionalitat o una racionalitat acotada en els jugadors. Malgrat el nom, la teoria evolutiva de jocs no pressuposa necessàriament en sentit biològic. La teoria evolutiva de jocs inclou les evolucions biològica i cultural i també modela l' aprenentatge individual.
Normativa
El dilema del presoner
|
Cooperar | Traicionar |
| Cooperar |
article 22
|
03
|
| Traicionar |
article 3
|
article 1
|
D'altra banda, alguns matem√†tics no veuen la teoria de jocs com una eina que prediu la conducta dels √©ssers humans, sin√≥ com un suggeriment sobre com s'haurien de comportar. At√®s que l' equilibri de Nash constitueix la millor resposta a les accions d' altres jugadors, seguir una estrat√®gia que √©s part de l' equilibri de Nash sembla el m√©s apropiat. Tanmateix, aquest √ļs de la teoria de jocs tamb√© ha rebut cr√≠tiques. En primer lloc, en alguns casos √©s apropiat jugar segons una estrat√®gia aliena a l'equilibri si un espera que els altres tamb√© jugaran d'acord a l'equilibri. Per exemple, en el joc¬†adivina 2/3 de la mitjana.
El dilema del presoner presenta un altre contraexemple potencial. En aquest joc, si cada jugador persegueix el seu propi benefici ambdós jugadors obtenen un resultat pitjor que de no haver-ho fet. Alguns matemàtics creuen que això demostra la fallida de la teoria de jocs com una recomanació de la conducta a seguir.
 
Psicologia i Psiquiatria
Els dissenys experimentals amb base en jocs d' intercanvi econ√≤mic han comen√ßat a utilitzar-se per a l' estudi de persones amb trastorns psiqui√†trics i la comprensi√≥ del funcionament neural que subjau als processos cognitius i de processament afectiu; fent √®mfasi en la presa de decisions, entre dues o m√©s persones davant la possibilitat de distribuir b√©ns econ√≤mics5En aquest sentit, se sap que les persones prenen decisions en els jocs econ√≤mics d' acord a la seva capacitat per experimentar¬†confian√ßa,6‚Äč7‚Äč8aix√≠ com el seu processament impl√≠cit9i expl√≠cit de la confiabilitat dels seus companys.
Biologia
Falcó-Paloma
|
Falcó | Colom |
| Falcó |
(V-C)/2
(V-C)/2 |
V0
|
| Colom |
0V
|
V/2V
/2 |
A difer√®ncia de l' √ļs de la teoria de jocs en l' economia, les recompenses dels jocs en¬†biologia s' interpreten freq√ľentment com¬†a adaptaci√≥. A m√©s, el seu estudi s' ha enfocat menys en l' equilibri que correspon a la noci√≥ de racionalitat, centrant-se en l' equilibri mantingut per les forces¬†evolutives. L'equilibri m√©s ben conegut en biologia es coneix com¬†a estrat√®gia evolutivament estable, i va ser introdu√Įt per primera vegada per¬†John Maynard Smith. Tot i que la seva motivaci√≥ inicial no comportava els requisits mentals de l' equilibri de Nash, tota estrat√®gia evolutivament estable √©s un equilibri de Nash.
En biologia, la teoria de jocs s'empra per entendre molts problemes diferents. Es va utilitzar per primera vegada per explicar l'evolució (i estabilitat) de les proporcions de sexes 1:1 (mateix nombre de mascles que de femelles). Ronald Fisher va suggerir el 1930 que la proporció 1:1 és el resultat de l'acció dels individus tractant de maximitzar el nombre dels seus néts subjectes a la restricció de les forces evolutives.
Cal recalcar que, els biòlegs han usat la teoria de jocs evolutiva i el concepte d'estratègia evolutivament estable per explicar el sorgiment de la comunicació animal (John Maynard Smith i Harper l'any 2003). L' anàlisi de jocs amb senyals i altres jocs de comunicació ha proporcionat noves interpretacions sobre l' evolució de la comunicació en els animals.
Finalment, els biòlegs han usat el problema falcó-colom (també conegut com a problema de la gallina) per analitzar la conducta combativa i la territorialitat.
Informàtica i lògica
La teoria de jocs ha començat a desenvolupar un paper important en la lògica i la informàtica. Moltes teories lògiques s'assenten en la semàntica de jocs. A més, els investigadors d'informàtica han usat jocs per modelar programes que interactuen entre si.
Ciència política
La investigaci√≥ en ci√®ncia pol√≠tica tamb√© ha usat resultats de la teoria de jocs. Una explicaci√≥ de la¬†teoria de la pau democr√†tica √©s que el debat p√ļblic i obert a la democr√†cia envia informaci√≥ clara i fiable sobre les intencions dels governs cap a altres estats. D'altra banda, √©s dif√≠cil con√®ixer els interessos dels l√≠ders no democr√†tics, quins privilegis atorgaran i quines promeses mantindran. Segons aquest raonament, hi haur√† desconfian√ßa i poca cooperaci√≥ si almenys un dels participants d'una disputa no √©s una democr√†cia.10‚Äč
L' aplicaci√≥ de teoria de jocs, en ci√®ncia pol√≠tica s' est√©n en altres √†rees com la¬†divisi√≥ equitativa, la¬†pol√≠tica econ√≤mica,¬†decisions p√ļbliques,¬†negociacions de guerra, teoria pol√≠tiques positives i la¬†teoria de l' elecci√≥ social. En cadascuna d'aquestes √†rees, els investigadors han desenvolupat models de teoria de jocs on els jugadors s√≥n votants, estats, grups d'inter√®s o burocr√†tics i pol√≠tics.
Alguns d'aquests exemples de teoria de jocs van ser explicats per¬†Anthony Downs. Al seu llibre¬†An Economic Theory of Democracy,11en el qual va aplicar la¬†Llei d'Hotelling al proc√©s pol√≠tic. En el model de Downsian, els candidats pol√≠tics perpetuen en ideologies en un espai de dimensi√≥ pol√≠tica. Downs primer mostra com els candidats pol√≠tics van a convergir a la ideologia preferida del votant mitj√† si els votants estan completament informats. Per√≤ llavors, argumenta que els votants trien romandre racionals ignorant el que permet que es doni la diverg√®ncia dels candidats. Tamb√©, va ser aplicada el 1962 en la crisi de missils de Cuba durant la presid√®ncia de John. F. Kennedy.12‚Äč
 
Dret Penal i Criminologia
Recentment, s'està abordant la utilitat de la teoria de jocs i les seves metodologies d'anàlisi per fonamentar la responsabilitat penal de les persones jurídiques (empreses, associacions, fundacions, etc.) i per a l'elaboració de models de predicció, detecció i reacció enfront de delictes comesos per directius i empleats en aquest tipus d'organitzacions. El jurista espanyol Rafael Aguilera ha estat pioner en aquesta línia d'investigació13en proposar en els seus estudis la utilització de la teoria de jocs i teories socioeconòmiques en el Dret Penal corporatiu i la Criminologia, en concret per a:
a) Erigir un¬†model antr√≤pic de responsabilitat penal de la persona jur√≠dica.14‚Äč
En aquesta representaci√≥ l'ens corporatiu no √©s una veritable entitat, independent i amb capacitat per autodirigir-se, sin√≥ que es configura pels punts (que s√≥n els individus de l'organitzaci√≥) i les constriccions, limitacions i procediments (representades per l√≠nies) que, en puritat, s√≥n decidides i configurades pels propis individus. La persona jur√≠dica no t√© capacitat de cometre un injust o de culpabilitat, sin√≥ que se li transfereix la responsabilitat, amb l' an√†lisi pr√®via de les constriccions. Es concep l'ens com a possible destinatari de la responsabilitat penal per la ¬ęvisibilitat¬Ľ que det√© en virtut de les constriccions i els propis individus que les originen i implementen. Si, arran d'una conducta delictiva d'un individu, s'aprecia la inexist√®ncia d'unes constriccions i procediments tendents a impedir delictes o s'observen que s√≥n defectuoses o afavoridores de la comissi√≥ d'il¬∑l√≠cits (representat per l√≠nies vermelles), s'est√† observant un d√®ficit organitzatiu, aspecte impl√≠cit en el ¬ęfet de connexi√≥¬Ľ i aix√≤ deriva en la transmissi√≥ de responsabilitat penal a la persona jur√≠dica.
Model antròpic de responsabilitat penal corporativa d' Aguilera.
b) L' elaboració de programes de prevenció de delictes o corporate compliance programs que possibilitin una resposta més eficaç enfront del delicte a l' empresa.
Aguilera aborda l' extraordinària utilitat de la teoria de jocs per a l' àmbit juridicopenal i criminològio empresarial, doncs permet un estudi rigorós de les dinàmiques d' actuació i la interacció de caràcter estratègic entre participants que actuen dirigits pels seus propis interessos.15La teoria de jocs permet explicar com els individus, a través del seu comportament racional i amb sustent en les interaccions amb d' altres, es doten de regulació o adopten determinades decisions. A més, la teoria de jocs ve acompanyada d'un valuós desenvolupament metodològic que possibilita l'anàlisi dels processos decisoris tenint en consideració elements tan importants per analitzar i dilucidar responsabilitats penals com les asimetries informatives i el compliment o incompliment de les normes per raons estratègiques (com ocorre, per exemple, en el famós Dilema del Presoner).
Igualment, Aguilera argumenta per què els Estats estan promovent, a través de la possibilitat d'exoneració de responsabilitat penal corporativa, la incorporació de la figura del compliance officer o oficial de compliment i és que aquesta teoria demostra matemàticament que el compliance officer minorarà la tendència a l'incompliment de les empreses o resta d'organitzacions (el que es coneix en teoria de jocs com a solució externa al dilema).
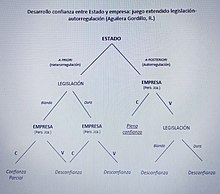
"En el dilema del presoner la desconfian√ßa √©s l'estrat√®gia dominant, la qual cosa condueix a un resultat negatiu per ambdues parts. En aquest cas, l' √≤rgan amb la¬†funci√≥ de compliance o¬†compliance officer permet adoptar el que s' anomena en la literatura una¬†soluci√≥ externa al dilema. Externa, no perqu√® aquest subjecte o departament especialitzat en compliment normatiu no pertanyi a l'ens, sin√≥ perqu√® el dilema nom√©s es resol amb la pres√®ncia d'aquest tercer element, ja que els jugadors per si sols ‚ÄďEstat i Empreses‚Äď no s√≥n capa√ßos de sortir del dilema, ja sigui perqu√® les persones jur√≠diques no compleixen, ja perqu√® l'Estat es veu obligat (amb els costos i recursos afegits que tot aix√≤ implica) a promulgar una legislaci√≥ dura. En altres paraules, l'√≤rgan amb la¬†funci√≥ de compliance o¬†compliance officer vigila i controla perqu√® en les persones jur√≠diques es compleixi i no es produeixi el dilema del presoner". Aguilera Gordillo, R.; Compliance Penal a Espanya, Ed. Thomson Reuters Aranzadi, 2018, pp. 238-239.
Aquest autor defensa que la teoria de jocs √©s totalment assumible i extraordin√†riament √ļtil per elaborar programes de prevenci√≥ de delictes o corporat compliance programes m√©s efica√ßos, ja que possibiliten la predicci√≥ de conductes il¬∑l√≠cites en tenir en compte aspectes com els fluxos d'informaci√≥, les relacions interpersonals, els aspectes t√†ctics respecte a altres individus o grups d'individus, aix√≠ com la pr√≤pia influ√®ncia que exerceixen les organitzacions; s'analitzen els riscos des d'una √≤ptica din√†mica i viva, com √©s la pr√≤pia realitat empresarial i no des de l'habitual perspectiva est√†tica (que √©s com tradicionalment s'ha vingut fent a trav√©s de l'√ļs de les cl√†ssiques matrius de risc).
El resultat d'utilitzar la teoria de jocs en el context empresarial √©s l'obtenci√≥ d'una major clarificaci√≥ de l'ampli elenc de conductes que pot realitzar cada treballador segons el lloc que ocupa, no de manera a√Įllada i est√†tica, sin√≥ tenint en consideraci√≥ que la decisi√≥ de cada empleat penja, al seu torn de decisions d'altres empleats -decisions estrat√®giques en entorns din√†mics-. D'aquesta manera, es pot resoldre, per exemple, com actuaria un empleat que s'ocupa de la comptabilitat d'una empresa o un altre la funci√≥ de la qual √©s subscriure els contractes de compra amb tercers; amb fonament en aquesta informaci√≥ global que t√© en compte tots els factors estrat√®gics (d'acord amb una metodologia cient√≠ficament contrastada) es poden establir uns procediments singulars que ¬ęobliguin¬Ľ cada membre de l'empresa a actuar d'una manera o altra segons els subjectes que van intervenir, circumst√†ncies concretes i context per respectar el marc legal. L'aplicaci√≥ de la teoria de jocs en l'elaboraci√≥ de programes de prevenci√≥ de delictes juntament amb la jurimetria permet obtenir el que Aguilera anomena un model d'organitzaci√≥ i gesti√≥ o compliance jurim√®tric. √Čs a dir, l'autor defensa que l'√ļs de la modelitzaci√≥ per elaborar compliance m√©s efectius per combatre els delictes a les empreses.
A més, la utilització d' aquesta metodologia per elaborar un corporat compliance program o programa de prevenció de delictes evidencia que, en l' organització, es té un ferm compromís amb la prevenció del delicte i el compliment normatiu, la qual cosa multiplica les opcions d' exclusió o lliurada de responsabilitat penal a la pròpia persona jurídica quan algun dels seus membres va aconseguir cometre un delicte.
D' altra banda, l' autor relaciona la utilitat de la teoria de jocs amb l' actual auge de programes i eines inform√†tiques d' an√†lisi de riscos, costos i beneficis en els processos de presa de decisions empresarials. Aquests programes fan √ļs d' una ingent quantitat de dades i realitzen milions d' operacions matem√†tiques tenint en consideraci√≥ el conjunt de decisions possibles, totes les seves conseq√ľ√®ncies i l' elenc d' estrat√®gies a adoptar; els seus resultats auguren informaci√≥ molt preciada, per exemple, quina √©s la decisi√≥ que comporta m√©s perill, quina √©s la m√©s conservadora, la m√©s costosa, etc. Al cap i a la fi, es tracta de la translaci√≥ al llenguatge inform√†tic de models matem√†tics i metodologia que porten les pr√≤pies teories economicistes, la teoria de jocs o el nou institucionalisme de l' elecci√≥ racional. √Čs a dir, des de la inform√†tica tamb√© ve assumint la validesa i utilitat de les referides teories a l' hora d' analitzar i predir conductes dels individus en organitzacions. Tanmateix, aquesta vinculaci√≥ entre ambd√≥s √†mbits no es contempla des del pla juridicopenal. Referent a aix√≤, proposa una decidida assimilaci√≥ pel Dret Penal de les propostes desenvolupades en la investigaci√≥ permetria l' establiment del que l' Aguilera ve a denominar¬†nexe l√≤gic d' arrel socio-jur√≠dica, la qual cosa permetria abordar amb major solv√®ncia les dificultats, reptes legals i dilemes √®tics que plantegen i plantejaran l' √ļs d' aquestes noves eines inform√†tiques per les empreses.
Filosofia
La teoria de jocs ha demostrat tenir molts usos en¬†filosofia. A partir de dos treballs de¬†W. V. O. Quine publicats el¬†1960 i¬†1967,¬†David Lewis (1969) va utilitzar la teoria de jocs per desenvolupar el concepte filos√≤fic de¬†convenci√≥. D' aquesta manera, va proporcionar la primera an√†lisi del¬†coneixement com√ļ i el va emp√®nyer a analitzar jocs de coordinaci√≥. A m√©s, va ser el primer en suggerir que es podia entendre el¬†significat en termes de¬†jocs de senyals. Aquest suggeriment s'ha seguit per molts fil√≤sofs des de la feina de Lewis.16‚Äč
Leon Henkin, Paul Lorenzen i Jaakko Hintikka van iniciar una aproximació a la semàntica dels llenguatges formals que explica amb conceptes de teoria de jocs els conceptes de veritat lògica, validesa i similars. En aquesta aproximació els "jugadors" competeixen proposant quantificacions i instàncies d'oracions obertes; les regles del joc són les regles d'interpretació de les sentències en un model, i les estratègies de cada jugador tenen propietats de les quals tracta la teoria semàntica (ser dominant si i només si les oracions amb què es juga compleixen determinades condicions, etc.).
La caça del cérvol
|
Cérvol | Llebre |
| Cérvol |
3, 3 |
0, 2 |
| Llebre |
2, 0 |
2, 2 |
En¬†√®tica, alguns autors han intentat continuar la idea de¬†Thomas Hobbes de derivar la moral de l'inter√®s personal. At√®s que jocs com el dilema del presoner presenten un conflicte aparent entre la moralitat i l' inter√®s personal, explicar per qu√® la cooperaci√≥ √©s necess√†ria per a l' inter√®s personal √©s una component important d' aquest projecte. Aquesta estrat√®gia general √©s un component de la idea de¬†contracte social en¬†filosofia pol√≠tica (exemples a Gauthier 1987 i Kavka 1986).17‚Äč
Finalment, altres autors han intentat usar la teoria evolutiva de jocs per explicar el naixement de les actituds humanes davant la moralitat i les conductes animals corresponents. Aquests autors han buscat exemples en molts jocs, incloent-hi el dilema del presoner, la caça del cérvol, i el joc del tracte de Nash per explicar la raó del sorgiment de les actituds sobre la moral (vegeu Skyrms 1996, 2004; Sobirà i Wilson 1999).
M√ļsica
Un compositor que usa la teoria de jocs en les seves composicions és Iannis Xenakis, en les seves obres Duel o Stratégie.
Optimització de disseny
La teoria d' optimització de disseny dicta cinc principis característics d' un joc, sense els quals, aquest deixaria de poder ser cridat de tal forma:
- Regles: Han de ser fàcils d'entendre, però només a través de l'experiència ser completament dominades.
- Interacció (Participació): Els jugadors, per mitjà de la intervenció del món creat, s'han d'oblidar del món real.
- Oposició: El joc ha de ser balancejat. Es requereix habilitat per guanyar, no sort.
- Presa de Decisions: Totes les preses de decisions han de tenir un incitador d'interès i un mèrit per més petites que siguin.
- Meta: Un punt final al qual arribar. Ha d'anar acompanyat d'un increment d'emocions i tensió mentre el joc s'acosta a la seva conclusió.
Història de la teoria de jocs
La primera discussió coneguda de la teoria de jocs apareix en una carta escrita per James Waldegrave el 1713. En aquesta carta, Waldegrave proporciona una solució mínima d'estratègia mixta a una versió per a dues persones del joc de cartes le Her. Tanmateix no es va publicar una anàlisi teòrica de teoria de jocs en general fins a la publicació de Recherches sur les príncipes mathèmatiques de la théorie des richesses, d' Antoine Augustin Cournot el 1838. En aquest treball, Cournot considera un duopoli i presenta una solució que és una versió restringida de l'equilibri de Nash.
Tot i que l'an√†lisi de Cournot √©s m√©s general que el de Waldegrave, la teoria de jocs realment no va existir com a camp d'estudi a part fins que¬†John von Neumann va publicar una s√®rie d'articles el¬†1928. Aquests resultats van ser ampliats m√©s tard en el seu llibre de¬†1944, Theory of Games and Economic Behavior19‚Äč, escrit juntament amb¬†Oskar Morgenstern. Aquest treball cont√© un m√®tode per trobar solucions √≤ptimes per a jocs de suma zero de dues persones. Durant aquest per√≠ode, el treball sobre teoria de jocs es va centrar, sobretot, en teoria de jocs cooperatius. Aquest tipus de teoria de jocs analitza les estrat√®gies √≤ptimes per a grups d' individus, assumint que poden establir acords entre si sobre les estrat√®gies m√©s apropiades.
El¬†1950 Albert W. Tucker va plantejar formalment les primeres discussions del¬†dilema del presoner, i es va emprendre un experiment sobre aquest joc a la corporaci√≥¬†RAND. Aquell any¬†John Nash va desenvolupar una definici√≥ d'una estrat√®gia √≤ptima per a jocs de m√ļltiples jugadors on l'√≤ptim no s'havia definit pr√®viament, conegut com¬†a equilibri de Nash, sota la supervisi√≥ de l'esmentat Tucker. Aquest equilibri √©s prou general, permetent l' an√†lisi de jocs no cooperatius a m√©s dels jocs cooperatius.
La teoria de jocs va experimentar una notable activitat en la dècada de 1950, moment en el qual els conceptes base, el joc de forma extensiva, el joc fictici, els jocs repetitius, i el valor de Shapley van ser desenvolupats. A més, en aquell temps, van aparèixer les primeres aplicacions de la teoria de jocs en la filosofia i les ciències polítiques.
El 1965, Reinhard Selten va introduir el seu concepte de solució dels equilibris perfectes del subjug i el concepte d'equilibri perfecte de mà tremolosa, que més endavant van refinar el concepte d'equilibri de Nash. El 1967 John Harsanyi va desenvolupar els conceptes de la informació completa i dels jocs bayesians. Ell, juntament amb John Forbes Nash i Reinhard Selten, van guanyar el Premi en Ciències Econòmiques en memòria d'Alfred Nobel el 1994.
En la¬†d√®cada de 1970 la teoria de jocs es va aplicar extensament a la¬†biologia, en gran part com a resultat del treball de¬†John Maynard Smith i el seu concepte estrat√®gia estable evolutiva. A m√©s, els conceptes de l' equilibri correlacionat,¬†equilibri perfecte de m√† temblorosa, i del coneixement com√ļ van ser introdu√Įts i analitzats.20‚Äč
El 2005, els teòrics de jocs Thomas Schelling i Robert Aumann van guanyar el Premi en Ciències Econòmiques en memòria d'Alfred Nobel. Schelling va treballar en models dinàmics, els primers exemples de la teoria de jocs evolutiva. Per la seva banda, Aumann va contribuir més a l'escola de l'equilibri.
El 2007, Roger Myerson, juntament amb Leonid Hurwicz i Eric Maskin, van rebre el Premi en Ciències Econòmiques en memòria d'Alfred Nobel per "seure les bases de la teoria de disseny de mecanismes."
El 2012, Lloyd Stowell Shapley i Alvin E. Roth guanyen el Premi en Ciències Econòmiques en memòria d'Alfred Nobel per donar nom dins d'aquest camp a mitja dotzena de teoremes, algoritmes, principis, solucions i índexs.
Vegeu també
Bibliografia
Referències generals
- Bierman, H. S. i L. Fernández, Game Theory with economic applications, Addison-Wesley, 1998.
- Davis, M. D. (1971): Introducció a la teoria de jocs. Aliança Editorial, 1a edició.
- Fudenberg, Drew i Jean Tirole: Game Theory, MIT Press, 1991, ISBN 0-262-06141-4.
- Gardner, R. (1996): Jocs per a empresaris i economistes. Antoni Bosh editors, 1a edició.
- Gibbons, Robert (1992): Game Theory for Applied Economists, Princeton University Press ISBN 0-691-00395-5. També publicat a Londres per Harvester Wheatsheaf (Londres) amb el títol A primer in game theory.
- Gibbons, R. (1993): Un primer curs de teoria de jocs. Antoni Bosch editors, 1a edició.
- Ginits, Herbert (2000): Game Theory Evolving. Princeton University Press, ISBN 0-691-00943-0.
- Osborne, Martin i Ariel Rubinstein: A Course in Game Theory, MIT Press, 1994, ISBN 0-262-65040-1.
- Rasmusen, Erik: Games and information, 4a edició, Blackwell, 2006. Disponible a Internet a http://www.rasmusen.org/GI/index.html.
- William Poundstone: El Dilema del Prisionero, Alianza Editorial, 2005.
- Cano, Mauricio, Mena L., Carlos i Sadka, Joyce (2009): "Teoria de Jocs i Dret Contemporani; Temes Selectes", ITAM, George Mason University i Porr√ļa.¬†ISBN 978-607-9-00031-8.
- Hillier, Frederick S. Introducció a la recerca d' operacions. Mèxic, D.F. : McGraw-Hill, c2010.
Lectures addicionals
- Binmore, K. (1994): Teoria de jocs. Editorial McGraw-Hill, 1a edició.
- Friedman, J.W. (1991): Teoria de jocs amb aplicacions a l'economia. Editorial Alianza Universidad.
- Kreps, D.M. (1994): Teoria de jocs i modelació econòmica. Fons de Cultura Econòmica, 1a edició.
- Tirole, J. (1990): La teoria de l'organització industrial. Editorial Ariel, 1a edició.
Textos d' importància històrica
- Fisher, Ronald (1930) The Genetical Theory of Natural Selection. Clarendon Press, Oxford.
- Luce, Duncan i Howard Raiffa Games and Decisions: Introduction and Critical Survey. Dover, ISBN 0-486-65943-7.
- Maynard Smith, John: Evolution and the Theory of Games, Cambridge University Press, 1982.
- Morgenstern, Oskar i John von Neumann (1947): Theory of Games and Economic Behavior. Princeton University Press.
- Nash, John (1950) "Equilibrium points in n-person games" Proceedings of the National Academy of the USA 36(1):48-49.
- Poundstone, William Prisoner's Dilemma: John von Neumann, Game Theory and the Puzzle of the Bomb, ISBN 0-385-41580-X.
Notes
- ‚ÜĎ De com la teoria matem√†tica dels jocs d'estrat√®gia resoldr√† els problemes de l'Eurozona i furar√† les armes nuclears iranianes, Ariel Rubinstein, 5 de maig de 2013, sense perm√≠s.
- ‚ÜĎ Gametheory.net t√© una extensa llista de refer√®ncies a la teoria de jocs en la cultura popular.
- ‚ÜĎ Alguns estudiosos consideren certs jocs asim√®trics com a exemples d'aquest tipus de jocs. Tanmateix, les recompenses m√©s habituals per a tots aquests jocs s√≥n sim√®triques.
- ‚ÜĎ El treball experimental en teor&a de jocs rep molts noms: econom&a experimental, econom&a conductista i teor&a conductista de jocs. Per a discussions recents en aquest camp vegeu Camer 2003.
- ‚ÜĎ Sanfey, A. G. (26 d'octubre de 2007).¬†¬ęSocial Decision-Making: Insights from Game Theory and Neuroscience¬Ľ.¬†Science 318 (5850): 598-602.¬†ISSN 0036-8075.¬†doi:10.1126/science.1142996. Consultat el 8 de mar√ß de 2019.
- ‚ÜĎ Unoka, Zsolt; √Čssers, Imola; √Āsp√°n, Nikoletta; B√≥di, Nikoletta; K√©ri, Szabolcs (2009-08).¬†¬ęTrust Game Reveals Restricted Interpersonal Transactions in Patients With Borderline Personality Disorder¬Ľ.¬†Journal of Personality Disorders 23 (4): 399-409.¬†ISSN 0885-579X.¬†doi:10.1521/pedi.2009.23.4.399. Consultat el 8 de mar√ß de 2019.
- ‚ÜĎ King-Casas, B.; Sharp, C.; Lomax-Bream, L.; Lohrenz, T.; Fonagy, P.; Montague, P. R. (8 d'agost de 2008).¬†¬ęThe Rupture and Repair of Cooperation in Borderline Personality Disorder¬Ľ.¬†Science (en angl√®s) 321 (5890): 806-810.¬†ISSN 0036-8075.¬†PMC 4105006.¬†PMID 18687957.¬†doi:10.1126/science.1156902. Consultat el 8 de mar√ß de 2019.
- ‚ÜĎ Berg, Joyce; Dickhaut, John; McCabe, Kevin (1995-7).¬†¬ęTrust, Reciprocity, and Social History¬Ľ.¬†Games and Economic Behavior (en angl√®s) 10 (1): 122-142.¬†doi:10.1006/game.1995.1027. Consultat el 8 de mar√ß de 2019.
- ‚ÜĎ van 't Wout, M.; Sanfey, A.G. (2008-9).¬†¬ęFriend or foe: The effect of implicit trustworthiness judgments in social decision-making¬Ľ.¬†Cognition (en angl√®s) 108 (3): 796-803.¬†doi:10.1016/j.cognition.2008.07.002. Consultat el 8 de mar√ß de 2019.
- ‚ÜĎ http://papers.ssrn.com/sol3/papers.cfm?abstract_id=433844
- ‚ÜĎ Plantilla:Harvard citations
- ‚ÜĎ Steven J. Brams,¬†Game theory and the Cuban missile crisis, Plus Magazine, 1 January 2001, accessed 31 January 2016.
- ‚ÜĎ Aguilera Gordillo, Rafael.¬†¬ęDissenyen nou model per prevenir responsabilitat penal de les empreses¬Ľ.¬†La Vanguardia.
- ‚ÜĎ Aguilera Gordillo, R. (2018).¬†Compliance Penal a Espanya. Thomson Reuters Aranzadi.¬†ISBN 978-84-9197-188-7.
- ‚ÜĎ Aguilera Gordillo (2019).¬†¬ęCompliance i Teoria de Jocs¬Ľ.¬†El Pa√≠s / Cinc Dies.
- ‚ÜĎ Skyrms 1996, Grim et al. 2004.
- ‚ÜĎ Per a una discussi√≥ detallada de l'√ļs de la teoria de jocs en √®tica vegeu l'entrada de la Stanford Encyclopedia of Philosophy,¬†teoria de jocs i √®tica.
- ‚ÜĎ Tony Crilly (2011).¬†50 coses que cal saber sobre matem√†tiques. Ed. Ariel.¬†ISBN 978-987-1496-09-9.
- ‚ÜĎ Teoria de jocs i del comportament econ√≤mic.
- ‚ÜĎ Tot i que el coneixement com√ļ va ser discutit per primera vegada pel fil√≤sof David Lewis en la seva dissertaci√≥¬†Convention a finals de la d√®cada de 1960, no es va estudiar amb deteniment pels economistes fins al treball de Robert Aumann, el 1970.
Enllaços externs
En espanyol
En anglès





Comentaris publicats
Afegeix-hi un comentari: