.PI

10-04-2019 (757 lectures)

La lletra grec en minúscula πs'utilitza com a símbol de Pi

Una circumferència de diàmetre 1 té perímetre

{stylestyle scripts {pi}}

scriptstyle {pi}

En matemàtiques , el nombre $pi$ és una relació numèrica definida per la relació entre la circumferència d'unacircumferència i el seu diàmetre ; és a dir, si una circumferència té un perímetre ${estil d'estil p}$ $p$ i diàmetre $d}$ $d$ , llavors aquest nombre és igual a ${estil d'estil p / d}$ ${estil d'estil w / d}$ . Està representat per la lletra grega π. La lletra grega π (llegeix: pi ) va ser adoptada per al nombre de la paraula grega per a perímetre, "περίμετρος", probablement per William Jones el 1706 i popularitzada per Leonhard Euleruns anys més tard. Altres noms per a aquesta constant són circulars constants o nombre de Ludolph .

Notació

El primer a utilitzar la lletra grega $pi$ eren els matemàtics anglesos, però per designar la circumferència d’un cercle. El primer que va utilitzar la definició actual ^[ 1 ] va ser William Jones . No obstant això, només va ser després que Leonhard Euler usés que hi havia acceptació de la notació per part de la comunitat científica. ^[ 2 ]

Valor de $pi$

El valor de $pi$ pertany als nombres irracionals . Per als càlculs més senzills és habitual aproximar-se ${stylestyle {pi}}$ ${pi}$ per 3.14. Bona part de les calculadores científiques de 8 dígits $pi$ per 3.114.926. Per calcular les rutes de navegació interplanetària, la NASA utilitza ${stylestyle pi: aprox. 3.141592653589793}$ ${estil estil pi: aprox. 3.141592653589793}$ (fins als 15 decimals) [1] . Per calcular un cercle amb 46 mil milions de anys llum de la llum al voltant de l’ univers observable, una aproximació de $pi$ amb només 40 decimals per assegurar l’exactitud d’un àtom d’hidrogen [2] .

Un enginyer japonès i un estudiant nord-americà en informàtica han calculat, mitjançant un ordinador amb dotze nuclis físics, cinc bilions de dígits, que equivalen a 6 terabytes de dades. ^[ 3 ]

Aproximació del nombre pi al decimal tricentenari: ${stylestyle scripts {pi}}$ $scriptstyle {pi}$ = 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165 27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273

Aproximacions a $pi$

Des de l' Antiguitat, s'han trobat diverses aproximacions $pi$ per calcular l’àrea del cercle. ^[ 4 ] Entre els egipcis, per exemple, al papir d'Ahmes , el valor atribuït a $pi$ seria ${displaystyle esquerra ({frac {4} {3} a la dreta} 4}$ ${displaystyle left ({frac {4} {3} fins a la dreta} 4}$ encara que també es troba el valor ${mostrar estil 3 {frac {1} {6}}.$ ${estil 3 {frac {1} {6}}.$ ^[ 5 ] ^[ 6 ] A la Bíblia (1 Reis 7:23), és possible trobar que els hebreus utilitzen el valor ${stylestyle 3}$ $3$ com a aproximació de $pi$ . ^[ 5 ] ^[ 7 ] Entre els babilonis, era habitual utilitzar el valor ${stylestyle 3}$ $3$ per calcular l’àrea del cercle, encara que sigui el valor ${mostrar estil 3 {frac {1} {8}}}$ ${display style 3 {frac {1} {8}}$ ja s’anomenen aproximacions. ^[ 4 ]

Mètodes de càlcul

Hi ha moltes maneres d’obtenir el valor aproximat de $pi$ mitjançant mètodes numèrics. Considerem això $pi$ és un nombre irracional i transcendent, de manera que els mètodes de càlcul impliquen sempre aproximacions, aproximacions successives i / o sèries infinites de sumes, multiplicacions i divisions.

Mètode clàssic per calcular $pi$

Mètode clàssic per calcular

pi

El primer intent rigorós de trobar $pi$ es deu a un dels matemàtics més coneguts de l' Antiguitat , Arquimedes .Mitjançant la construcció de polígons inscrits i circumscrits de 96 costats es va trobar que pi seria entre un valor entre 223/71 i 22/7, és a dir, seria aproximadament entre 3.1408 i 3.1429. Aquest mètode és l’anomenat mètode clàssic per calcular el pi. ^[ 8 ]

Ptolomeu , que vivia a Alexandria aproximadament al segle III dC, calculava sobre la base d’un polígon de 720 costats inscrit en una circumferència de 60 unitats de radi. El seu valor era aproximadament de 3.1416. Tenint en compte el que sabem ara, el seu enfocament era molt millor que el d’Arquimedes.

La "cerca" per al valor de ${stylestyle {pi}}$ ${pi}$ va arribar a Xina , on Liu Hui , una copiadora de llibres, va aconseguir obtenir el valor de 3.114159 amb un polígon de 3.072 cares. Però només a finals del segle V el matemàtic Tsu Ch'ung Chih va arribar a una millor aproximació: entre 3.1415926 i 3.1415927.

En aquest mateix moment, el matemàtic hindú Aryabhata va escriure en versos en un llibre la següent declaració: "Afegiu 4 a 100, multipliqueu per 8 i afegiu-ne 62.000. El resultat és aproximadament una circumferència de diàmetre 20.000".

Analitzant matemàticament i considerant l’equació ${stylestyle c = pi CD d:}$ $c =? d:$

(4 + 100) 8 + 62000 pi 200 {20000}

(4 + 100) 8 8 + 62000 200 2000 Dret

{stylestyle 104 cdot 8 + 62000 pi 20020 Rightarrow}

104? 8 + 62000? 200000?

{Mostra estil 832 + 62000 pi CDOT 20000 Rightarrow}

832 + 62000 pi 200 20000

{displaystyle 62832 pi CDOT 20000 Rightarrow}

62832 pi cdot 20000 Rightarrow

{62832 sobre 20000}

{62832 més de 20000} pi

El valor de ${stylestyle {pi},}$ $pi,$ per tant, seria 3.1416 . Bviament, com més gran sigui el nombre de decimals, millor serà l’aproximació del valor real de pi. Però hem de tenir en compte que, aleshores, no era fàcil de calcular.

El major càlcul de decimals fins al segle XV va ser 3.11415926535897932 pel matemàtic àrab Ghiyath al-Kashi . El matemàtic holandès Ludolph van Ceulen , a finals del segle XVI , va calcular una ${stylestyle {pi}}$ ${pi}$ amb 35 decimals, començant per un polígon de 15 costats, duplicant el nombre de costats 37 vegades i després augmentant el nombre de costats. Per curiositat, la seva dona tenia gravada la tomba a la ciutat ${stylestyle {pi}}$ ${pi}$ amb els 35 decimals esmentats anteriorment.

Avui en dia és relativament més fàcil, amb ordinadors moderns calculant fins a trilions de decimals per a ${stylestyle {pi}.}$ $pi.$

Una aproximació de ${stylestyle {pi}}$ ${pi}$ que presenta una diferència d'aproximadament ${Mostra estil 2 {,}} 7 \times 10-7}$ ${Mostra l'estil 2 {,}} 7 × 10-7}$ és el següent:

{355 sobre 113}

{355 més de 113} pi

Formulació matemàtica del mètode d'Arquimedes edita el codi font

Basant-se en el mètode d' Arquímedes és possible formular una representació matemàtica per calcular el pi, eficient per a un polígon de qualsevol nombre de costats.

Tenint en compte un polígon de n costats i el radi 1, tenim la mesura del costat expressat per la llei dels cosinus :

$a2 = b2 + c2 -2bc) alfa}$ $a ^ 2 = b ^ 2 + c ^ 2 - 2bc cos?$

Hem format un triangle isòsceles, base $l}$ $l$ i els costats ${stylestyle r = 1}$ $r = 1$ :

${estil l2 = r2 + r2 -2r2) alfa}$ $2 = r ^ 2 + r ^ 2 - 2 ^ 2 cos?$

$l 2 = 1 2 + 1 2 -2 cos?$ $1 ^ 2 = 1 ^ 2 + 1 ^ 2 - 2 amb?$

$l 2 = 2-2 alfa}$ $l 2 = 2-2 cos$

$l = {sqrt {2-2) cos alfa}}}$ $l = sqrt {2 - 2 cos alfa}$

L' angle del triangle isòsceles al centre del polígon s'expressa en 360 ° dividit pel nombre de costats $n}$ $n$ , per tant:

$l = {sqrt {2-2 cos cos esquerra ({frac {360} {n}}}}}}$ $l = sqrt {2 - 2 cos a l'esquerra (360 {n} a la dreta)}$

D'aquesta manera, el perímetre del polígon serà:

$p = n. {sqrt {2-2 cos cos esquerra ({frac {360} {n}}}}}}$ $p = n sqrt {2 - 2 cos a l'esquerra (360 {n} a la dreta)}$

Com? $pi$ està representat pel perímetre del polígon dividit pel seu diàmetre , tenim:

${stylestyle pi = {frac {n} {sqrt {2-2) cos esquerra {{360} {n}}}}} {2}}}$ $2 = 2 cos a l'esquerra (fracció {360} {n})}} {2}$

Aplicant transformacions trigonomètriques, la fórmula anterior es pot simplificar:

${stylestyle pi = n. operatorname {sen} a l'esquerra ({frac {180} {n}} a la dreta)}$ ${estilisme pi = n. operatorname {sen} a l'esquerra {{frac {180} {n}} a dreta}}$

Mètodes estadístics [ editar | edita el codi font

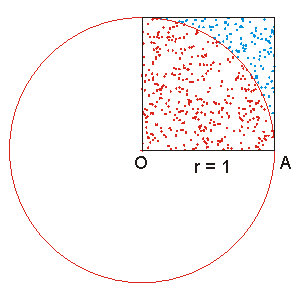
Metode estadístic Montecarlo per a càlcul d'uniq - postMath-00000039-QINU

Un altre mètode interessant per calcular $pi$ es pot realitzar a través de Monte Carlo utilitzant les estadístiques . En aquest mètode es dibuixen punts aleatoris en un quadrat entre les coordenades ${stylestyle O = (0,0)}$ $O = (0, 0)$ i $B = (1,1).}$ $B = (1, 1).$ Llavors es calcula la distància dels punts dibuixats ${stylestyle c_ {n} = (x n, y n}}$ $c_n = (x_n, y_n)$ a l’origen O = (0, 0). $pi$ es pot aproximar pel nombre de punts inscrits a la circumferència del radi 1 en relació amb el total de punts dibuixats al costat 1 del quadrat.

A l’exemple cap al costat, $386/500 = 3.088}$ $pi 4 386/500 = 3.088$

Un altre mètode que utilitza les estadístiques de Monte Carlo per al càlcul de $pi$ es coneix com Buffon's Needle , proposada al segle XVIII pel naturalista francès Georges de Buffon .

Mètodes de sèries infinites

El francès François Viète , que estudiava el mètode d 'Arquimedes, va desenvolupar la sèrie següent per al càlcul de $pi$ el 1593:

{frac {2} {sqrt {2}} {2} {sqrt {2}} 2 + {sqrt {2} {sqrt {2}}}}} {2}} cdot points = {frac {2} {pi}}

Sqrt {2} sqrt {2} sqrt {2} sqrt {2} 2}} {2} punts = frac {2} {pi}

El matemàtic John Wallis va desenvolupar una altra sèrie infinita el 1655:

{frac {2} {1}} {frac {2} {3}} {frac {4} {3} {frac {4} {5}} (1) i (2), (2) i (4), respectivament. dots = {frac {pi} {2}}.

? 2 {1}? {3} 2? {4} {3} {4} {5} {6} {5} {} frac {6} {7} {7} agost {8} {9} {punteja frac = {pi} {2}.

Una altra sèrie coneguda per al càlcul de $pi$ va ser desenvolupat per Leibniz el 1682, utilitzant la sèrie de Taylor per a la funció ${stylestyle arctan (x)}$ ${estilisme arctan (x)}$ , prenent ${stylestyle x = 1}$ ${estil x = 1}$ i, per tant, $arctan (1) = {frac {pi} {4}}}$ ${estil de visualització visual arctan (1) = {frac {pi} {4}}}$ .

suma n = 0} {infty} {frac {(-1) n} {2n + 1}} = 1 - {1} {3} frac {1} {5}} {{1} {7}} {{1} {9}} - punts = {frac {pi} {4}}}}

sum_ {n = 0} frac {(1) ^ n} {2n + 1} = 1 - {1} {3} + {1} {5} - {1} {7} + {1} {9} - bats frac = {pi} {4}.

Johann Heinrich Lambert va publicar, el 1770, una sèrie en forma de divisions infinites:

{Mostra {4} {frac {4} {pi} = 1 + {frac {1 2} {3 + {2 2} {5 + { 2} {7 + {4 2} {9 + {frac {5} {11 + {frac {6}}} }}}}}

1 2 3 4 5 2 3 4 5 2 3 4 5 2 3 4 5 2 3 4 3 4 4 4 4 4 4 5 4 5 6 7 4 4 4 5 6 7 8 9 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 [9+? 5 ^ 2 ^ {11 + {6} {2}

Mètodes de càlcul numèric

Un dels estudis dels mètodes de càlcul numèric és obtenir l’arrel d’una funció. Quan considerem la funció ${stylestyle f (x) = sin (x)}$ ${estil estil f (x) = sin (x)}$ ho sabem $f (pi) = sin (pi) = 0.$ $estil de visualització f (pi) = sin (pi) = 0.$ Els principals mètodes del càlcul numèric per obtenir la funció arrel ${stylestyle f (x)}$ $f (x)$ pot incloure una cerca binària al rang ${stylestyle [a, b]}$ $[a, b]$ on ho sabem $f (3) = sin (3)> 0}$ ${estil de visualització f (3) = sin (3)> 0}$ $(a = 3)}$ $(a = 3)$ i $f (4) = sin (4) <0}$ ${estil de visualització f (4) = sin (4) <0}$ $(b = 4)}$ $(b = 4)$ llavors podem perfeccionar l’interval a:

{Mostra estil a la dreta [a, {{a + b} sobre 2} a la dreta],}

{Mostra l'estil a dreta [a, {{a + b} sobre 2} a dreta],}

{Mostra estil f a l'esquerra ({{a + b} sobre 2} a la dreta) <0}

{Mostra l'estil fa l'lumbra ({{a + b} sobre 2} a la dreta) <0}

{stylestyle esquerra [{{a + b} sobre 2}, b dret],}

{estilisme restant {2},}}

{mostrar estil f a l'esquerra ({{a + b} sobre 2} a la dreta)

{mostra l'estil fa l'esquerra ({{a + b} el 2} a la dreta)

Sortida des de l’abast ${stylestyle pi a [3,4]}$ $pi [3,4]$ aquest mètode us permet afinar-lo successivament als intervals

${stylestyle pi a [3.3.3]}$ $pi a [3, 3.5]$
${stylestyle pi a [3.3.25]}$ $pi a [3, 3.25]$
${stylestyle pi a [3.125.3.25]}$ $pi a [3.125, 3.25]$
${stylestyle pi a [3.125.3.1875]}$ $pi a [3.125, 3.1875]$

i així successivament.

Encara en el càlcul numèric, el mètode de Newton-Raphson , més eficient que una cerca binària, permet obtenir aproximacions successives a l'arrel de la funció ${stylestyle f (x) = sin (x)}$ ${estil estil f (x) = sin (x)}$ utilitzant un punt de partida ${estil x_ {0}}$ $x_0$ que requereix que sàpiguem ${stylestyle f '(x) = cos (x).}$ ${estil estil f '(x) = cos (x).}$

Prendre's a tu mateix ${estil x_ {0} = 3}$ $x_0 = 3$ i tenint en compte això per Newton-Rapson

${estil x_ {i + 1} = x_ {i} - {{f (x i}} sobre {f '(x_ {i}} = = x_ {i} - {{ {i})} sobre {cos (xi)}} = x_ {i} - {(xi)}}$ $(xi) = {xi} - {{xi}} {{f (xi}}} sobre {cos (xi )}} = x_ {i} - {(xi)}}$

tenim les següents sèries per a $pi$

${estil x_ {0} = 3}$ $x_0 = 3$
${stylestyle x_ {1} = 3.14254654}$ $x_1 = 3.14254654$
${stylestyle x_ {2} = 3.14159265}$ $x_2 = 3.14159265$

Un mètode de càlcul numèric optimitzat per al càlcul de $pi$ a través de les arrels d’una funció es pot obtenir simplificant

{estil x_ {i + 1} = x_ {i} + sin (x_ {i})}

{estil x i + 1 = x i + sin (x i)

perquè a les rodalies de ${stylestyle pi,}$ $pi,$ $cos (x_ {i}) cong -1.}$ ${estil de visualització visual (xi) cong -1.}$ ^[ 9 ]

Tingueu en compte que en aquests algorismes de càlcul numèric es considera $pi$ com a transcendent, des de la funció ${stylestyle f (x) = sin (x)}$ ${estil estil f (x) = sin (x)}$ no es pot escriure a través d'un polinomi finit de coeficients racionals; la funció ${stylestyle f (x) = sin (x)}$ ${estil estil f (x) = sin (x)}$ s'obté mitjançant l’expansió de la sèrie de Taylor .

Algorisme de Gauss-Legendre

Yasumasa Kanada va utilitzar l’ algorisme de Gauss-Legendre , ^[ 10 ], que és un mètode numèric d’aproximacions successives ^[ 11 ] per obtenir el rècord mundial en el càlcul de llocs decimals de pi el 2002 . ^[ 12 ]

Mètode de càlcul aïllat de decimals ${stylestyle {pi}}$ ${pi}$

El 1995 , David Harold Bailey , en col·laboració amb Peter Borwein i Simon Plouffe , va descobrir una fórmula per calcular π, una suma infinita (sovint anomenada fórmula BBP ):

{stylestyle pi = suma {k = 0} {frac {1} {16k}} a l'esquerra {4} {8k + 1}} 8k + 4} - {frac {1} {8k + 5}} {{1k + 6}}}

(8k + 1) - {8k + 4} - {1k + 1} - {1k + 4} 1 (8k + 5) - {1k + 6}

Aquesta fórmula us permet calcular fàcilment el desè primer binari decimal o hexadecimal de ${stylestyle {pi}}$ ${pi}$ sense haver de calcular els decimals anteriors. El lloc de Baileyconté la seva derivació i implementació en diversos llenguatges de programació. Gràcies a una fórmula derivada de la fórmula BBP , els 4 000 000 000 000 000 000 $pi$ base es va obtenir el 2001 .

Quantitats que depenen de $pi$

Diverses relacions matemàtiques depenen del coneixement de la constant ${stylestyle pi,}$ $pi,$ els més coneguts a nivell didàctic són:

Perímetre d'un cercle : $C = 2$ $C = 2?$
Àrea del cercle: $A = pi2}$ $A = pi RT2$
Volum d'una esfera : $V = {4 sobre 3}$ $V = {4 a 3} piot r ^ 3$

Atès que la superfície de l’esfera és ${estil S = 4 pi r2}$ $S = 4 pi r2$ , $pi$ també es troba en les fórmules gravitacionals i l' electromagnetisme de la física ${displaystyle left (F = {1 sobre 4 cdot epsilon0} Q {q sobre d2}}}$ ${displaystyle left (F = {1 a 4 cdot epsilon0} Q {q a d2}}}$ .

Irracionalitat i transcendència de $pi$

El perímetre de la circumferència és de 3.1416 ... vegades més gran que el diàmetre, sent la relació perímetre / diàmetre

pi

(pi)

Johann Heinrich Lambert ho va demostrar el 1761 ${stylestyle x}$ $x$ és racional i diferent de ${displaystyle 0}$ ${displaystyle 0}$ , així que tampoc ${estil d'estudi (x)}$ ${estil d'estud (x)}$ cap ${estil d'estudi i x}$ $ix$ pot ser racional. Com? ${stylestyle an esquerre ({frac {pi} {4}} dret) = 1}$ ${estil d'estil un residu {{frac {pi} {4} dret} = 1}$ , segueix això ${frac {pi} {4}}}$ ${estil visual {frac {pi} {4}}}$ és irracional , i per tant $pi$ és irracional. ^[ 13 ] ^[ 14 ]

Lindemann ho va demostrar el 1882 $pi$ és transcendent usant el mètode Hermite utilitzat per demostrar que e és transcendent.Això vol dir que $pi$ no pot ser la solució de cap equació algebraica de coeficients racionals . La transcendència de ${stylestyle {pi}}$ ${pi}$ estableix la impossibilitat de resoldre el problema de la quadratura del cercle : és impossible construir, només amb regle euclidià i compàs , un quadrat la zona del qual és estrictament igual a la zona d'un cercle donat.

Preguntes sense resposta

La pregunta oberta més important és si ${stylestyle {pi}}$ ${pi}$ és un nombre normal , és a dir, si apareix alguna dada de successió de dígits ${stylestyle {pi},}$ $pi,$ com es podria esperar d’una seqüència de figures infinita i completament aleatòria. Això hauria de ser cert en qualsevol base , no només a la base 10.

Tampoc se sap que les figures apareixen un nombre infinit de vegades en la constitució de ${stylestyle {pi}.}$ $pi.$

Bailey i Crandall van demostrar el 2000 que l'existència de la fórmula Bailey-Borwein-Plouffe abans esmentada i fórmules similars impliquen la normalitat de ${stylestyle {pi}}$ ${pi}$ a la base 2.

Cronologia del càlcul de $pi$

Matemàtic	Any	Llocs decimals
Egipcis ( Papir Rhind )	1650 aC	1
Arquimedes	250 AC	3
Zu Chongzhi	480 DC	7
Ghiyath al-Kashi	1424	16
Ludolph van Ceulen	1596	35
Georg von Vega	1794	126
Gauss	1824	200
William Shanks	1874	527
Levi B. Smith, John W. Wrench	1949	1.120
Daniel Shanks, John W. Wrench	1961	100.265
Jean Guilloud, M. Bouyer	1973	1.000.000
Yasumasa Kanada , Sayaka Yoshino, Yoshiaki Tamura	1982	16.777.206
Yasumasa Kanada, Yoshiaki Tamura, Yoshinobu Kubo	1987	134,217,700
Chudnovskys	1989	1.011.169.691
Yasumasa Kanada, Daisuke Takahashi	1997	51.539.600.000
Yasumasa Kanada, Daisuke Takahashi	1999	206.158.430.000
Yasumasa Kanada	2002	1.241.100.000.000
Daisuke Takahashi	2009	2.576.980.370.000 ^[ 15 ]
Fabrice Bellard	2010	2.699.999.990.000 ^[ 16 ]
Shigeru Kondo i Alexander Yee	2010	5.000.000.000.000 ^[ 17 ]
Shigeru Kondo i Alexander Yee	2011	10.000.000.000.050 ^[ 17 ]
Shigeru Kondo	2013	12,100,000,000,050 ^[ 17 ]
Emma Haruka Iwao	2019	31,415,926,535,897 ^[ 18 ]

Vegeu també

Wikipedia té un article sobre:
Portal de matemàtiques

Wikimedia Commons té suports relacionats amb: Pi

Notes

↑ És a dir, que π és un nombre que representa la relació entre el perímetre d'una circumferència i el seu diàmetre
(Eves (2004) pàg. 144
↑ "PC de 18.000 $ EUA calcula 5 bilions de números de Pi"
^{Ir para:A} ^b Cajori (2007), pàg. 45
(A ^b Eves (2004), pàg. 141
↑ Boyer (1996), pàg. 12
↑ El número Pi de la Bíblia
(Eves (2004), pàg. 141 i 142
↑ "El càlcul del nombre pi" (PDF) . 2006 . Obtingut el 13 d’octubre de 2007
Smith Harry J. Smith (20 d'octubre de 2004). "Algorisme de Gauss-Legendre" .Obtingut el 29 de gener de 2008
Felipe, Enrique (12 d'abril de 2018). "Algorisme iteratiu Gauss-Legendre per al càlcul de Pi" . Consultat el 22 de març de 2019
↑ «Yasumasa Kanada» . 10 de desembre de 2002 . Obtingut el 29 de gener de 2008
Ori Cajori (2007), pàg. 330
↑ Boyer (1996), pàg. 320
↑ «El nostre últim disc es va establir com a continuació»
» « Registre de computació Pi »
^{Ir para:A} ^b ^c «Número mundial»
^ Mia, Neagle (14 de març de 2019). "Una recepta per batre el registre de les xifres més calculades de pi" . Google Blog . Consultat el 22 de març de 2019

Bibliografia

BOYER, CB (1996). Història de les matemàtiques . Editora Edgard Blücher . [Sl: sn] ISBN 85-212-0023-4
CAJORI, F. (2007). Història de les matemàtiques . Editora Ciência Moderna . [Sl: sn] ISBN 978-85-7393-555-4
EVES, H. (2004). Introducció a la història de les matemàtiques . Editor Unicamp . [Sl: sn] ISBN 85-268-0657-2

Enllaços externs

Curiositats de les matemàtiques - Evolució cronològica del càlcul de pi
pi amb 10.000 dígits - La Universitat d'Utah (en anglès )
Pi, el símbol matemàtic més notable.

versió per imprimir

DARRERS ARTICLES COMENTATS

	1.	Mal d'ull
	2.	Faiança
	3.	EL PROGRESO CATALAN EN AMERICA
	4.	Corona d'Aragó o Corona de Catalunya
	5.	Els 20 millors invents de tots els temps
	6.	La fal·làcia de la sortida de Palos o d'altres llocs de l'estret
	7.	Conferència: 'LA CARTA DE COLOM I L'ADN'
	8.	El gascó-borgonyó-català Llengua universal a Europa i Navarra-Basconia del s.XIII al s.XV
	9.	Guerau Ponç de Cabrera
	10.	Català i occità, diferents en 13 punts

EL MÉS COMENTAT

	1.	Flat Earth Society
	2.	Cat_Colom: quatre viatges
	3.	Mal d'ull
	4.	Els 20 millors invents de tots els temps
	5.	El ciao italiano i el siau catalán
	6.	Corona d'Aragó o Corona de Catalunya
	7.	Efecte Coanda
	8.	FRANCESC ALBÓ DE RODAS - PRIMER EN EMPRAR UNA 'CATENA A POPA'
	9.	La fal·làcia de la sortida de Palos o d'altres llocs de l'estret
	10.	Corsaris barbarescs

EL MÉS LLEGIT

	1.	Història de les armes de foc
	2.	Rathaus -Ulm -Catalonia
	3.	Mapes de Dieppe
	4.	Benet Viñes Martorell - Uracans
	5.	La Raor de Llull: Una Troballa Lingüística i Històrica
	6.	Pany de Miquelet
	7.	Història del llibre
	8.	Intel·ligència humana - HI
	9.	Catalan Discovery of Australia
	10.	PROVA QUE LA BANDERA BORBÒNICA DERIVA DE LA SENYERA

.PI

Notació

Valor de $pi$

Aproximacions a $pi$

Mètodes de càlcul

Mètode clàssic per calcular $pi$

Formulació matemàtica del mètode d'Arquimedes edita el codi font

Mètodes estadístics [ editar | edita el codi font

Mètodes de sèries infinites

Mètodes de càlcul numèric

Algorisme de Gauss-Legendre

Mètode de càlcul aïllat de decimals ${stylestyle {pi}}$ ${pi}$

Quantitats que depenen de $pi$

Irracionalitat i transcendència de $pi$

Preguntes sense resposta

Cronologia del càlcul de $pi$

Vegeu també

Notes

Bibliografia

Enllaços externs

Enllaços

Articles

Sabies que...?

.PI

Notació

Valor de

Aproximacions a

Mètodes de càlcul

Mètode clàssic per calcular

Formulació matemàtica del mètode d'Arquimedes edita el codi font

Mètodes estadístics [ editar | edita el codi font

Mètodes de sèries infinites

Mètodes de càlcul numèric

Algorisme de Gauss-Legendre

Mètode de càlcul aïllat de decimals {stylestyle {pi}}

Quantitats que depenen de

Irracionalitat i transcendència de

Preguntes sense resposta

Cronologia del càlcul de

Vegeu també

Notes

Bibliografia

Enllaços externs

Enllaços

Articles

Sabies que...?

Valor de $pi$

Aproximacions a $pi$

Mètode clàssic per calcular $pi$

Mètode de càlcul aïllat de decimals ${stylestyle {pi}}$ ${pi}$

Quantitats que depenen de $pi$

Irracionalitat i transcendència de $pi$

Cronologia del càlcul de $pi$