Donada la seva llarga història, hi ha nombroses demostracions (més de 350) del teorema de Pitàgores, potser més que qualsevol altre teorema de matemàtiques.

Les proves següents no són exhaustives, i s'han agrupat principalment pels enfocaments utilitzats en les proves.

La prova feta per Pitàgores

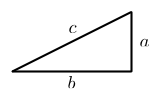
Qualsevol triangle rectangle amb potes $un$ i $b$ la hipotenusa $c$ com l'anterior, utilitzeu-ne quatre per fer un quadrat amb costats $un+b$ com es mostra a continuació:

Forma un quadrat al centre amb longitud lateral $c$ i, per tant, una àrea de c^2.c2.

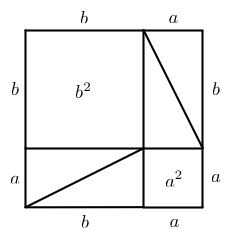
No obstant això, si reordenem els quatre triangles de la següent manera, podem veure dos quadrats dins del quadrat més gran, un que és a^2un2 en el terreny i un que és b^2b2 a la zona:

Atès que la plaça més gran té la mateixa àrea en ambdós casos, és a dir, (a+b)^2(un+b)2, i atès que els quatre triangles també són els mateixos en ambdós casos, hem de concloure que els dos quadrats a^2un2 i b^2b2 de fet, són iguals en superfície a la plaça més gran c^2c2.

Així a^2 + b^2 = c^2un2+b2=c2. _quadrat□​

La demostració feta per Euclides

En resum, així és com procedeix la demostració en els Elements d'Euclides. El gran quadrat es divideix en un rectangle a l'esquerra i un rectangle dreta. Es construeix un triangle que té la meitat de l'àrea del rectangle esquerre. A continuació, es construeix un altre triangle que té la meitat de l'àrea del quadrat a la part esquerra. Aquests dos triangles es mostren congruents, demostrant que aquest quadrat té la mateixa àrea que el rectangle esquerre. Aquest argument va seguit d'una versió similar per al rectangle dret i el quadrat restant. Ajuntant els dos rectangles per reformar el quadrat sobre la hipotenusa, la seva àrea és la mateixa que la suma de les àrees dels altres dos quadrats. Els detalls segueixen.

Deixar $A,B,C$ ser els vèrtexs d'un triangle rectangle amb l'angle recte a $A.$ Deixa anar una perpendicular des de $UN$ al costat del quadrat oposat a la hipotenusa del triangle (com es mostra a continuació). Aquesta línia divideix el quadrat de la hipotenusa en dos rectangles, cadascun amb la mateixa àrea que un dels dos quadrats de les cames.

Per a la prova formal, necessitem quatre lemmata elementals:

1. Si dos triangles tenen dos costats de l'un igual a dos costats de l'altre, cadascun a cada un, i els angles inclosos per aquests costats iguals, llavors els triangles són congruents (costat-angle-costat).
2. L'àrea d'un triangle és la meitat de l'àrea de qualsevol paral·lelogram sobre la mateixa base i que té la mateixa altitud.
3. L'àrea d'un rectangle és igual al producte de dos costats adjacents.
4. L'àrea d'un quadrat és igual al producte de dos dels seus costats (segueix de 3).

A continuació, cada quadrat superior està relacionat amb un triangle congruent amb un altre triangle relacionat al seu torn amb un dels dos rectangles que componen el quadrat inferior.

Deixar $ACB$ és un triangle d'angle recte amb angle recte $CAB$.

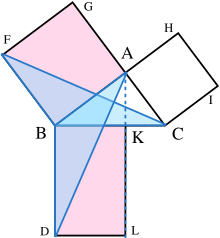
En cadascun dels costats $BC$, $AB$i $AA$, es dibuixen quadrats: $CBDE$, $BAGF$i $ACIH$, en aquest ordre. La construcció de quadrats requereix els teoremes immediatament anteriors en Euclides i depèn del postulat paral·lel.

De $UN$, dibuixa una línia paral·lela a $BD$ i $CE$. Es creuarà perpendicularment $BC$ i $DE$ a $K$ i $L$respectivament.

Unir $CF$ i $ANUNCI$, per formar els triangles $BCF$ i $BDA$.

Angles $CAB$ i $BAG$ són els dos angles rectes; per això $C$, $UN$i $G$ Són col·lineals. De la mateixa manera per $B$, $UN$i $H$.

Angles $CBD$i $FBA$ són els dos angles rectes; per tant, angle $ABD$ és igual a angle $FBC$, ja que ambdós són la suma d'un angle recte i un angle $ABC$.

Des que $AB$ és igual a $FB$ i $BD$ és igual a $BC$triangle $ABD$ ha de ser congruent amb el triangle $FBC$.

Des que $UN$-$K$-$L$ és una línia recta paral·lela a $BD$rectangle $BDLK$ té el doble d'àrea de triangle. $ABD$ perquè comparteixen la base $BD$ tenen la mateixa altitud $BK$, és a dir, una línia normal a la seva base comuna, connectant les línies paral·leles $BD$ i $AL$. (Lemma 2 més amunt)

Des que $C$ col·lina amb $UN$ i $G$quadrat $BAGF$ ha d'estar dues vegades en àrea a triangle $FBC$.

Per tant, rectangle $BDLK$ ha de tenir la mateixa àrea que la plaça BAGF, BAGF, el que és AB^2.UNB2.

De la mateixa manera, es pot demostrar que el rectangle $CKLE$ ha de tenir la mateixa àrea que la plaça ACIH, ACIH, el que és AC^2.UNC2.

Si s'afegeixen aquests dos resultats, AB^2 + AC^2 = BD times BK + KL times KC.UNB2+UNC2=BD×BK+KL×KC.

Des que $BD=KL$, $BD×BK+KL×KC=BD(BK+KC)=BD×BC.$

Per això AB^2 + AC^2 = BC^2UNB2+UNC2=BC2 des que $CBDE$ és una plaça. _quadrat□​

Ús de triangles similars

Deixar $ABC$ representen un triangle rectangle, amb l'angle recte situat a $C$, com es mostra a la figura. Dibuixa l'altitud des del punt $C$, i truca $D$ la seva intersecció amb el costat $AB$. Punt $D$ divideix la longitud de la hipotenusa $c$ en parts $d$ i $e$. El nou triangle $ACD$ és similar al triangle $ABC$, perquè tots dos tenen un angle recte (per definició de l'altitud), i comparteixen l'angle a $UN$, és a dir, que el tercer angle $($que anomenarem $θ)$ El mateix passarà en ambdós triangles. Per un raonament similar, el triangle $CBD$ també s'assembla al triangle. $ABC$. La demostració de similitud dels triangles requereix el postulat del triangle: la suma dels angles d'un triangle és de dos angles rectes, i és equivalent al postulat paral·lel. La similitud dels triangles condueix a la igualtat de relacions dels costats corresponents:

dfrac {BC}{AB} = dfrac {BD}{BC} ~~ text{ and } ~~ dfrac {AC}{AB} = dfrac {AD}{AC}.ABBC​ =BCBD​ i ABAC​=ACANUNCI​.

Les fraccions de la primera igualtat són els cosinus de l'angle. $θ$, mentre que els de la segona igualtat són els seus pecats. Aquestes relacions es poden escriure com

BC^2 = AB times BD ~~ text{ i } ~~ AC^2 = AB times AD.BC2=AB×BD i A C2=AB×AD.

Sumant aquestes dues igualtats es tradueix en

AC^2 + BC^2 = AB(BD + AD) = AB^2.UNC2+BC2=AB(BD+ANUNCI)=UNB2.

Per això

AC^2 + BC^2 = AB^2. _quadratUNC2+BC2=UNB2. □​

Dues demostracions algebraiques que utilitzen quatre conjunts de triangles

El teorema es pot demostrar algebraicament utilitzant quatre còpies d'un triangle rectangle amb costats. $un$, $b,$ i $c$ disposada a l'interior d'una plaça amb costat $c,$ Com a la meitat superior del diagrama. Els triangles són similars a l'àrea. {frac {1}{2}ab}21​ab, mentre que el quadrat petit té un costat $b−un$ i àrea (b - a)^2(b−un)2. La superfície de la gran plaça és, per tant,

(b-a)^{2}+4{frac {ab}{2}}=(b-a)^{2}+2ab=a^{2}+b^{2}.(b−un)2+42ab​=(b−un)2+2ab=un2+b2.

Es tracta d'una plaça amb costat $c$ i àrea c^2c2tan

c^{2}=a^{2}+b^{2}.c2=un2+b2.

Una demostració similar utilitza quatre còpies del mateix triangle disposades simètricament al voltant d'un quadrat amb el costat c, com es mostra a la part inferior del diagrama. Això dóna com a resultat un quadrat més gran amb costat $un+b$ i àrea (a + b)^2(un+b)2. Els quatre triangles i el quadrat amb el costat $c$ ha de tenir la mateixa àrea que la plaça més gran:

(b+a)^{2}=c^{2}+4{frac {ab}{2}}=c^{2}+2ab,(b+un)2=c2+42ab​=c2+ 2ab,

donant

c^{2}=(b+a)^{2}-2ab=a^{2}+b^{2}.c2=(b+un)2−2ab=un2+b2.

Una prova relacionada va ser publicada pel futur president dels Estats Units James A. Garfield. En lloc d'un quadrat, utilitza un trapezi, que es pot construir des del quadrat en la segona de les proves anteriors biseccionant al llarg d'una diagonal del quadrat interior, per donar el trapezi com es mostra en el diagrama. L'àrea del trapezi es pot calcular com la meitat de l'àrea de la plaça, és a dir,

{frac {1}{2}} (b+a)^{2}.21​(b+un)2.

El quadrat interior es redueix a la meitat i només hi ha dos triangles, de manera que la prova procedeix com a dalt excepte per a un factor de frac{1}{2}21​, que s'elimina multiplicant per dos per donar el resultat. _quadrat□​