Cercle de confusió - Optics - La vaca cega desconfiada

02-10-2010 (582 lectures)

Categoria: Optics

Cercle de confusió - Optics

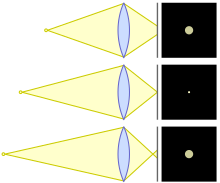
Diagrama que mostra cercles de confusió per a la font del punt massa a prop, en el focus i massa lluny

En òptica, un cercle de confusió és una taca òptica causada per un con de raigs de llum d'una lent que no arriba a un enfocament perfecte a l'hora d'imaginar una font puntual. També es coneix com a disc de confusió, cercle d'indistinció, cercle de desenfocament o punt de desenfocament.

En fotografia, el cercle de confusió (CoC) s'utilitza per determinar la profunditat de camp, la part d'una imatge que és acceptablement nítida. Sovint s'associa un valor estàndard de CoC a cada format d'imatge, però el valor més adequat depèn de l'agudesa visual, les condicions de visualització i la quantitat d'ampliació. Els usos en context inclouen el cercle màxim permès de confusió, el límit de diàmetre del cercle de confusió i el criteri del cercle de confusió.

Les lents reals no enfoquen perfectament tots els raigs, de manera que, fins i tot en el millor dels casos, un punt s'imagina com un punt en lloc d'un punt. El punt més petit que pot produir una lent sovint es coneix com el cercle de menys confusió.

Dos significats

Cal distingir dos usos importants d'aquest terme i concepte:

En una lent $L$ perfecta, tots els raigs passen a través d'un punt focal $F$ . No obstant això, a altres distàncies de la lent els raigs formen un cercle.

Per descriure el punt de desenfocament més gran que és indistingible des d'un punt. Una lent pot enfocar amb precisió els objectes a una sola distància; els objectes a altres distàncies es desenfocen. Els punts d'objecte desenfocats s'imaginen com a taques de desenfocament en lloc de punts; com més gran sigui la distància d'un objecte del pla d'enfocament, més gran serà la mida de la taca de desenfocament. Aquesta taca borrosa té la mateixa forma que l'obertura de la lent, però per simplicitat, se sol tractar com si fos circular. A la pràctica, els objectes a distàncies considerablement diferents de la càmera encara poden aparèixer nítids; ^[1] el rang de distàncies dels objectes sobre els quals els objectes semblen nítids és la profunditat de camp (DoF). El criteri comú per a la "nitidesa acceptable" a la imatge final (per exemple, impressió, pantalla de projecció o visualització electrònica) és que el punt de desenfocament sigui indistingible des d'un punt.
En una lent imperfecta $L$ , no tots els raigs passen per un punt focal. El cercle més petit que passen per $C$ s'anomena cercle de menys confusió.

Per descriure el punt de desenfocament aconseguit per una lent, en el seu millor enfocament o més generalment. Reconeixent que les lents reals no enfoquen tots els raigs perfectament en les millors condicions, el terme cercle de menys confusió s'utilitza sovint per al punt de desenfocament més petit que pot fer una lent,^[2] per exemple escollint una millor posició d'enfocament que comprometi les diferents distàncies focals efectives de diferents zones de lents a causa d'aberracions esfèriques o d'altres. El terme cercle de confusió s'aplica de manera més general, a la mida del punt fora d'enfocament al qual una lent mostra un punt d'objecte. Els efectes de difracció de l'òptica d'ones i l'obertura finita d'una lent determinen el cercle de menor confusió; ^[3] l'ús més general del "cercle de confusió" per a punts fora de focus es pot calcular purament en termes d'òptica de raigs (geomètrics). ^[4]

En l'òptica de raigs idealitzada, on se suposa que els raigs convergeixen fins a un punt quan estan perfectament enfocats, la forma d'un punt de desenfocament des d'una lent amb obertura circular és un cercle de llum de vora dura. Un punt de desenfocament més general té vores suaus a causa de la difracció i les aberracions,^[5]^[6] i pot ser no circular a causa de la forma d'obertura. Per tant, el concepte de diàmetre s'ha de definir acuradament per tal de ser significatiu. Les definicions adequades sovint utilitzen el concepte d'energia encerclada, la fracció de l'energia òptica total del punt que es troba dins del diàmetre especificat. Els valors de la fracció (per exemple, 80%, 90%) varien amb l'aplicació.

Cercle de confusió límit de diàmetre en fotografia

En fotografia, el cercle de límit de diàmetre de confusió (límit CoC o criteri coC) sovint es defineix com la taca de desenfocament més gran que encara serà percebuda per l'ull humà com un punt, quan es visualitza en una imatge final des d'una distància de visió estàndard. El límit de CoC es pot especificar en una imatge final (per exemple, una impressió) o en la imatge original (en una pel·lícula o sensor d'imatge).

Amb aquesta definició, el límit de CoC de la imatge original (la imatge de la pel·lícula o sensor electrònic) es pot establir en funció de diversos factors:

Agudesa visual. Per a la majoria de la gent, la distància de visualització còmoda més propera, anomenada distància propera per a una visió diferent,^[7] és d'aproximadament 25 cm. A aquesta distància, una persona amb bona visió sol distingir una resolució d'imatge de 5 parells de línies per mil·límetre (lp/mm), equivalent a un CoC de 0,2 mm a la imatge final.
Condicions de visualització. Si la imatge final es visualitza a aproximadament 25 cm, sovint és adequat un CoC d'imatge final de 0,2 mm. Una distància de visió còmoda també és aquella en què l'angle de visió és d'aproximadament 60 °; ^[7] a una distància de 25 cm, això correspon a uns 30 cm, aproximadament la diagonal d'una imatge de 8 polzades × 10 polzades (per comparació, el paper A4 és de 8,3 en × 11,7 polzades, 210 mm × 297 mm; El paper de carta dels EUA és de 8,5 polzades × 11 polzades, 216 mm × 279 mm). Sovint pot ser raonable suposar que, per a la visualització d'imatges senceres, una imatge final de més de 8 en × 10 polzades es veurà a una distància corresponentment superior a 25 cm, i per a la qual pot ser acceptable un CoC més gran; el CoC de la imatge original és llavors el mateix que es determina a partir de la mida estàndard de la imatge final i la distància de visualització. Però si la imatge final més gran es veurà a la distància normal de 25 cm, caldrà un CoC d'imatge original més petit per proporcionar una nitidesa acceptable.
Ampliació des de la imatge original fins a la imatge final. Si no hi ha cap ampliació (per exemple, una impressió de contacte d'una imatge original de 8×10), el CoC de la imatge original és el mateix que el de la imatge final. Però si, per exemple, la dimensió llarga d'una imatge original de 35 mm s'amplia a 25 cm (10 polzades), el factor d'ampliació és d'aproximadament 7 i el CoC de la imatge original és de 0,2 mm / 7 o 0,029 mm.

És possible que els valors comuns del límit de CoC no siguin aplicables si les condicions de reproducció o visualització difereixen significativament de les assumides en la determinació d'aquests valors. Si a la imatge original se li donarà una major ampliació o es veurà a una distància més propera, caldrà un CoC més petit. Els tres factors anteriors s'adapten a aquesta fórmula:

CoC (en mm) = (distància de visualització (en cm) / 25 cm ) / (resolució d'imatge final desitjada en lp / mm per a una distància de visualització de 25 cm) / ampliació

Per exemple, per suportar una resolució d'imatge final equivalent a 5 lp/mm per a una distància de visualització de 25 cm quan la distància de visualització prevista és de 50 cm i l'ampliació prevista és de 8:

CoC = (50 / 25) / 5 / 8 = 0,05 mm

Atès que la mida final de la imatge no se sol conèixer en el moment de fer una fotografia, és habitual assumir una mida estàndard com ara 25 cm d'amplada, juntament amb un CoC d'imatge final convencional de 0,2 mm, que és 1/1250 de l'amplada de la imatge. També s'utilitzen habitualment convencions pel que fa a la mesura diagonal. El DoF calculat mitjançant aquestes convencions s'haurà d'ajustar si la imatge original es retalla abans d'ampliar-la a la mida final de la imatge o si s'alteren la mida i les suposicions de visualització.

Per a format de marc complet de 35 mm (24 mm × 36 mm, 43 mm de diagonal), un límit CoC àmpliament utilitzat és $d$ /1500, o 0,029 mm per a format de marc complet de 35 mm, que correspon a resoldre 5 línies per mil·límetre en una impressió de 30 cm en diagonal. Els valors de 0,030 mm i 0,033 mm també són habituals per al format de fotograma complet de 35 mm.

També s'han utilitzat criteris relacionats amb la CoC amb la distància focal de la lent. Kodak va recomanar 2 minuts d'arc (el criteri Snellen de 30 cicles/grau per a la visió normal) per a la visió crítica, donant un CoC d'aproximadament $f$ /1720, on $f$ és la distància focal de la lent. ^[8] Per a una lent de 50 mm en format full-frame de 35 mm, el CoC corresponent és de 0,0291 mm. Aquest criteri suposava evidentment que una imatge final es veuria a una distància correcta en perspectiva (és a dir, l'angle de visió seria el mateix que el de la imatge original):

Distància de visió = distància focal de presa de lents × ampliació

No obstant això, les imatges poques vegades es veuen a l'anomenada distància "correcta"; l'espectador normalment no coneix la distància focal de la lent de presa i la distància "correcta" pot ser incomfortablement curta o llarga. En conseqüència, els criteris basats en la distància focal de les lents generalment han donat pas a criteris (com $d$ /1500) relacionats amb el format de la càmera.

Si una imatge es visualitza en un suport de visualització de baixa resolució, com ara un monitor d'ordinador, la detectabilitat del desenfocament estarà limitada pel mitjà de visualització i no per la visió humana. Per exemple, el desenfocament òptic serà més difícil de detectar en una imatge de 8 en × 10 en un monitor d'ordinador que en una impressió de 8×10 de la mateixa imatge original vista a la mateixa distància. Si la imatge només s'ha de veure en un dispositiu de baixa resolució, pot ser adequat un CoC més gran; no obstant això, si la imatge també es pot veure en un mitjà d'alta resolució, com ara una impressió, regiran els criteris comentats anteriorment.

Les fórmules de profunditat de camp derivades de l'òptica geomètrica impliquen que qualsevol DoF arbitrari es pot aconseguir mitjançant l'ús d'un CoC prou petit. A causa de la difracció, però, això no és del tot cert. L'ús d'un CoC més petit requereix augmentar el nombre f de la lent per aconseguir el mateix DoF i, si la lent s'atura prou lluny, la reducció del desenfocament del desenfocament es compensa amb l'augment del desenfocament de la difracció. Vegeu l'article Profunditat de camp per a una discussió més detallada.

Cercle de confusió límit de diàmetre basat en d/1500

Diàmetre coC basat en $d$ /1500 per a diversos formats d'imatge
Format de la imatge	Classe de format	Mida del marc^[9]	CoC
Sensor d'1" (Nikon 1, Sony RX10, Sony RX100)	Petit format	8,8 mm × 13,2 mm	0,011 mm
Sistema de quatre terços		13,5 mm × 18 mm	0,015 mm
APS-C^[10]		15,0 mm × 22,5 mm	0,018 mm
Cànon APS-C		14,8 mm × 22,2 mm	0,018 mm
APS-C Nikon/Pentax/Sony		15,7 mm × 23,6 mm	0,019 mm
Cànon APS-H		19,0 mm × 28,7 mm	0,023 mm
35 mm		24 mm × 36 mm	0,029 mm
645 (6×4.5)	Format Mitjà	56 mm × 42 mm	0,047 mm
6×6		56 mm × 56 mm	0,053 mm
6×7		56 mm × 69 mm	0,059 mm
6×9		56 mm × 84 mm	0,067 mm
6×12 anys		56 mm × 112 mm	0,083 mm
6×17 anys		56 mm × 168 mm	0,12 mm
4×5	Gran Format	102 mm × 127 mm	0,11 mm
5×7 anys		127 mm × 178 mm	0,15 mm
8×10 anys		203 mm × 254 mm	0,22 mm

Ajust del diàmetre del cercle de confusió per a l'escala DoF d'una lent

El nombre f determinat a partir d'una escala DoF de lents es pot ajustar per reflectir un CoC diferent d'aquell en què es basa l'escala DoF. Es mostra a l'article Profunditat de camp que

{displaystyle mathrm {DoF} ={frac {2Ncleft(m+1right)}{m^{2}-left({frac {Nc}{f}}right)^{2}}},,}

on $N$ és el nombre f de la lent, $c$ és el CoC, $m$ és l'augment i $f$ és la distància focal de la lent. Com que el nombre f i coC es produeixen només com a producte $Nc$ , un augment d'un equival a una disminució corresponent de l'altre. Per exemple, si se sap que una escala DoF de lents es basa en un CoC de 0,035 mm i les condicions reals requereixen un CoC de 0,025 mm, el CoC s'ha de reduir per un factor de 0,035 / 0,025 = 1,4; això es pot aconseguir augmentant el nombre f determinat a partir de l'escala DoF pel mateix factor, o aproximadament 1 parada, de manera que la lent es pot tancar simplement 1 parada del valor indicat a l'escala.

Normalment es pot utilitzar el mateix enfocament amb una calculadora DoF en una càmera de visualització.

Determinació d'un cercle de diàmetre de confusió a partir del camp objecte

Diagrama de lents i raigs per calcular el cercle de confusió diàmetre

c

per a un subjecte fora d'enfocament a distància

S 2

quan la càmera està enfocada a

S 1

. El cercle de desenfocament auxiliar

C

en el pla de l'objecte (línia discontínua) facilita el càlcul.

Un primer càlcul del diàmetre de CoC ("indistinció") per "T.H." el 1866.

Per calcular el diàmetre del cercle de confusió en el pla de la imatge per a un subjecte fora de focus, un mètode és calcular primer el diàmetre del cercle de desenfocament en una imatge virtual en el pla de l'objecte, que simplement es fa mitjançant triangles similars, i després multiplicar per l'augment del sistema, que es calcula amb l'ajut de l'equació de la lent.

El cercle borrós, de diàmetre $C$ , en el pla de l'objecte enfocat a distància $S 1$ , és una imatge virtual no enfocada de l'objecte a distància $S 2$ tal com es mostra en el diagrama. Depèn només d'aquestes distàncies i del diàmetre de l'obertura $A$ , a través de triangles similars, independents de la distància focal de la lent:

{displaystyle C=A{|S_{2}-S_{1}| over S_{2}},.}

El cercle de confusió en el pla de la imatge s'obté multiplicant per ampliació $m$ :

{displaystyle c=Cm,,}

on l'augment $m$ ve donat per la relació de distàncies de focus:

{displaystyle m={f_{1} over S_{1}},.}

Utilitzant l'equació de lents podem resoldre per a la variable auxiliar $f 1$ :

{displaystyle {1 over f}={1 over f_{1}}+{1 over S_{1}},,}

quins rendiments

{displaystyle f_{1}={fS_{1} over S_{1}-f},,}

i expressar l'augment en termes de distància focalitzada i distància focal:

{displaystyle m={f over S_{1}-f},,}

que dóna el resultat final:

{displaystyle c=A{|S_{2}-S_{1}| over S_{2}}{f over S_{1}-f},.}

Això es pot expressar opcionalment en termes del nombre f $N = f/A$ com:

{displaystyle c={|S_{2}-S_{1}| over S_{2}}{f^{2} over N(S_{1}-f)},.}

Aquesta fórmula és exacta per a una lent prima paraxial simple o una lent simètrica, en la qual la pupil·la d'entrada i la pupil·la de sortida són ambdues de diàmetre $A$ . Els dissenys de lents més complexos amb un augment pupil·lar no unitari necessitaran una anàlisi més complexa, tal com s'aborda en profunditat de camp.

Més generalment, aquest enfocament condueix a un resultat paraxial exacte per a tots els sistemes òptics si $A$ és el diàmetre de la pupil·la d'entrada, les distàncies de l'assignatura es mesuren des de l'alumne d'entrada i es coneix l'augment:

{displaystyle c=Am{|S_{2}-S_{1}| over S_{2}},.}

Si la distància d'enfocament o la distància del subjecte fora de focus és infinita, les equacions es poden avaluar en el límit. Per a una distància d'enfocament infinita:

{displaystyle c={fA over S_{2}}={f^{2} over NS_{2}},.}

I per al cercle borrós d'un objecte a l'infinit quan la distància de focus és finita:

{displaystyle c={fA over S_{1}-f}={f^{2} over N(S_{1}-f)},.}

Si el valor $c$ es fixa com un cercle de límit de diàmetre de confusió, qualsevol d'aquests es pot resoldre perquè la distància del subjecte obtingui la distància hiperfocal, amb resultats aproximadament equivalents.

Història

Enric Coddington 1829

Abans d'aplicar-se a la fotografia, el concepte de cercle de confusió s'aplicava a instruments òptics com els telescopis. Coddington (1829, 54) quantifica tant un cercle de menys confusió com un cercle de confusió menor per a una superfície reflectant esfèrica.

Això podem considerar com l'aproximació més propera a un enfocament senzill, i anomenar el cercle de la menor confusió.

Societat per a la Difusió del Coneixement Útil 1832

La societat per a la difusió del coneixement útil (1832, p. 11) l'aplicava a aberracions de tercer ordre:

Aquesta aberració esfèrica produeix una indistinció de la visió, en estendre cada punt matemàtic de l'objecte en un petit punt de la seva imatge; quines taques, en barrejar-se entre si, confonen el tot. El diàmetre d'aquest cercle de confusió, al focus dels raigs centrals F, sobre el qual s'estén cada punt, serà L K (fig. 17.); i quan l'obertura del reflector és moderada és igual al cub de l'obertura, dividit pel quadrat del radi (...): aquest cercle s'anomena aberració de latitud.

T.H. 1866

Càlculs de cercles de confusió: Un precursor primerenc dels càlculs de profunditat de camp és la TH (1866, p. 138) càlcul d'un diàmetre de cercle de confusió a partir d'una distància de subjecte, per a una lent enfocada a l'infinit; aquest article va ser assenyalat per von Rohr (1899). La fórmula que planteja per al que ell anomena "la indistinció" és equivalent, en termes moderns, a

{displaystyle c={fA over S}}

per a la distància focal $f$ , el diàmetre de l'obertura $A$ i la distància del subjecte $S$ . Però no inverteix això per trobar la $S$ corresponent a un criteri $c$ donat (és a dir, no resol per la distància hiperfocal), ni considera enfocar a cap altra distància que l'infinit.

Finalment, observa que "les lents d'enfocament llarg solen tenir una obertura més gran que les curtes, i en aquest compte tenen menys profunditat d'enfocament" [el seu èmfasi cursiu].

Dallmeyer i Abney

Dallmeyer (1892, pàg. 24), en una reedició ampliada del seu pare John Henry Dallmeyer el 1874 (Dallmeyer 1874) pamflet Sobre l'elecció i l'ús de lents fotogràfiques (en material que no es troba a l'edició de 1874 i sembla haver estat afegit a partir d'un article de J.H.D. "Sobre l'ús de diafragmes o parades" de data desconeguda), diu:

Així, cada punt d'un objecte fora de focus està representat a la imatge per un disc, o cercle de confusió, la mida del qual és proporcional a l'obertura en relació amb el focus de la lent emprada. Si un punt de l'objecte és 1/100 d'una polzada fora de focus, es representarà mitjançant un cercle de confusió que mesura però 1/100 part de l'obertura de la lent.

Aquesta última afirmació és clarament incorrecta, o errònia, estant desactivada per un factor de distància focal (distància focal). Continua:

i quan els cercles de confusió són prou petits l'ull no els veu com a tals; després es veuen només com a punts i la imatge apareix nítida. A la distància ordinària de la visió, de dotze a quinze polzades, els cercles de confusió es veuen com a punts, si l'angle contingut per ells no supera el minut d'arc, o aproximadament, si no superen els 1/100 d'una polzada de diàmetre.

Numèricament, 1/100 polzades a 12-15 polzades està més a prop de dos minuts d'arc. Aquesta elecció del límit de CoC segueix sent (per a una impressió gran) la més utilitzada fins i tot avui en dia. Abney (1881, pp. 207–08) adopta un enfocament similar basat en una agudesa visual d'un minut d'arc, i tria un cercle de confusió de 0,025 cm per a la visualització a 40-50 cm, essencialment fent el mateix factor de dos errors en unitats mètriques. No està clar si Abney o Dallmeyer van ser abans per establir l'estàndard CoC d'aquesta manera.

Wall 1889

El límit comú de CoC de 1/100 polzades s'ha aplicat per desenfocar a part del desenfocament. Per exemple, Wall (1889, 92) diu:

Per trobar la rapidesa amb què ha d'actuar un obturador per prendre un objecte en moviment que pot haver-hi un cercle de confusió de menys de 1/100 polzades de diàmetre, dividiu la distància de l'objecte per 100 vegades el focus de la lent i dividiu la rapidesa de moviment de l'objecte en polzades per segon pels resultats, quan tingueu la durada més llarga de l'exposició en fracció de segon.

Vegeu també

Notes

^ Raig 2000, p. 50.
^ Ray 2002, p. 89.
^ J.-A. Beraldin; et al. (2006). "Reconstrucció virtual de llocs patrimonials: oportunitats i reptes creats per les tecnologies 3D". A Mans Baltsavias; Armin Gruen; Luc Van Gool; Maria Pateraki (eds.). Registre, modelització i visualització del patrimoni cultural. Taylor i Francesc. Pàg 145. ISBN 978-0-415-39208-2.
^ Walter Bulkeley Coventry (1901). La tècnica de la càmera de mà. Sorres i Co. p. 9.
^ Stokseth 1969, p. 1317.
^ Merklinger 1992, pp. 45–46.
^ Puja a:^un ^b Raig 2000, p. 52.
^ Kodak 1972, p. 5.
^ La mida del marc és una mitjana de càmeres que fan fotografies d'aquest format. Per exemple, no totes les càmeres 6×7 prenen fotogrames que són exactament de 56 mm × 69 mm. Consulteu les especificacions d'una càmera en particular si es necessita aquest nivell d'exactitud.
^ "APS-C" és un format comú per a les rèflex digitals. Les dimensions varien lleugerament entre diferents fabricants; per exemple, el format APS-C de Canon és nominalment de 15,0 mm × 22,5 mm, mentre que el format DX de Nikon és nominalment de 16 mm × 24 mm. Les dimensions exactes de vegades varien lleugerament entre models amb el mateix format nominal d'un fabricant determinat.

Referències

Abney, Sir William de Wiveleslie. 1881. Un tractat de fotografia. Londres: Longmans, Green and Co.
Coddington, Enric. 1829. Tractat sobre la Reflexió i Refracció de la llum: ser Part I. d'un Sistema d'Òptica. Cambridge: J. Smith.
Dallmeyer, John Henry. 1874. Sobre l'elecció i l'ús de lents fotogràfiques. Nova York: E. i H.T. Anthony and Co.
Dallmeyer, Thomas R. 1892. Sobre l'elecció i l'ús de lents fotogràfiques. Londres: J. Pitcher.
Companyia Eastman Kodak. 1972. Fórmules òptiques i la seva aplicació, Kodak Publicació núm. AA-26, Rev. 11-72-BX. Rochester, Nova York: Eastman Kodak Company.
Kodak. Veure Companyia Eastman Kodak.
Merklinger, Harold M. 1992. Les IN i OUTs de FOCUS: una forma alternativa d'estimar la profunditat de camp i la nitidesa en la imatge fotogràfica. v. 1.0.3. Bedford, Nova Escòcia: Seaboard Printing Limited. ISBN 0-9695025-0-8. Versió 1.03e disponible en PDF a http://www.trenholm.org/hmmerk/.
Ray, Sidney F. 2000. La geometria de la formació d'imatges. A The Manual of Photography: Photographic and Digital Imaging, 9a ed. Ed. Ralph E. Jacobson, Sidney F. Ray, Geoffrey G. Atteridge i Norman R. Axford. Oxford: Premsa Focal. ISBN 0-240-51574-9
Ray, Sidney F. 2002. Òptica Fotogràfica Aplicada, 3a ed. Oxford: Premsa Focal. ISBN 0-240-51540-4
Societat per a la Difusió del Coneixement Útil. 1832. Filosofia natural: amb una explicació de termes científics, i un índex. Londres: Baldwin i Cradock, Paternoster-Row.
Stokseth, Per A. 1969. Propietats d'un sistema òptic desenfocat. Revista de la Societat d'Òptica d'Amèrica 59:10, oct. 1969.
T.H. [pseud.]. 1866. "Enfocament llarg i curt". British Journal of Photography 13.
von Rohr, Moritz. 1899. Lent fotogràfica. Berlín: Verlag Julius Springer.
Mur, Edward John. 1889. Diccionari de fotografia per al fotògraf aficionat i professional. Nova York: E. i H. T. Anthony and Co.

Enllaços externs

Cercles de confusió per a càmeres digitals - DOFMaster
Depth of Field in Depth (PDF) - inclou discussió de cercle de criteris de confusió
Què és el "Cercle de confusió" - manual ƒ/Calc

versió per imprimir

Comentaris publicats

Afegeix-hi un comentari:

Nom a mostrar:

E-mail:

	Genera una nova imatge
Introduïu el codi de seguretat

Accepto les condicions d'ús següents:

Per a participar en els comentaris l'usuari es compromet a complir i acceptar les següents normes bàsiques de conducta:

Respectar les opinions de la resta dels participants al fòrum, tot i no compartir-les necessàriament.
Abstenir-se d'insultar o utilitzar un llenguatge ofensiu, racista, violent o xenòfob, i no tenir cap conducta contrària a la legislació vigent i a l'ordre públic.
No enviar cap contingut amb copyright sense el permís del propietari. Si es considera oportú facilitar continguts d'internet amb copyright, cal escriure la URL completa perquè els altres usuaris puguin enllaçar-hi i descarregar-se els continguts des de la pàgina propietària.
Publicitat: No es permet enviar continguts promocionals i/o publicitaris.