If you have a model globe then you probably should refer to it while reading this material. 
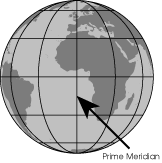
Notice that the globe has a network of vertical and horizontal lines. The horizontal lines are called parallels because they run parallel to each other, and the vertical lines are called meridians because any one shows all the places that have the same local time. Each location along a parallel has the same latitude, or distance from the equator. Each location along a meridian has the same longitude, or angle between it, the north pole, and the prime meridian.[1]
Latitude and longitude are two very different things: on the surface of the earth, latitude is a distance while longitude is an angle. You cannot tilt the earth on its side and expect the latitude lines to match the old longitude lines. The meridians converge to two points: the north and south poles, but the parallels don't converge anywhere; they stay the same distance apart everywhere.
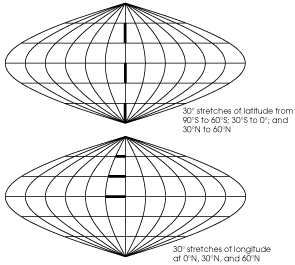

Every point on the globe has a meridian running through it from north to south and a parallel running through it from east to west. Maps and globes only show some of the meridians and parallels because if they showed all of them then the map would be black with lines and not very useful. Longitude and latitude are measured in degrees and marked with the ( ¬į ) symbol. There are 360 degrees of longitude, measured 180 degrees east and west of the prime meridian, and 180 degrees of latitude, measured 90 degrees north and south of the equator.
Taking the earth to be perfectly spherical,¬†one degree of latitude along a meridian (from one parallel to the next one 1¬į away) always measures the same distance because latitude measures distance. That distance amounts to about 111.1 km (69.1 mi) for the earth.
One degree of longitude on the other hand, measures angle, so the distance covered by 1¬į of longitude is a different distance at every latitude. Again taking the earth to be perfectly spherical, then at the equator 1¬į of longitude is the same as 1¬į of latitude; at 60¬į north or south the distance is half of that (55.6 km or 34.5 mi); and at either pole the distance is zero.
Minutes and seconds are used to measure smaller parts of a degree. Minutes are marked with ( ′ ) and seconds with ( ″ ). One minute is 1/60th of a degree and one second is 1/60th of a minute, so on the equator 1′ is about 1.85 km (1.15 mi) and 1″ is about 0.0309 km or 30.9 m (101 ft.)
The¬†coordinate of a location is given by the intersection of the parallel and meridian that pass through that location, along with a direction stating north or south for latitudes, or east or west for longitudes. Typically the latitude is given first. For example the point 35¬į40‚Ä≤45‚Ä≥N, 139¬į46‚Ä≤14‚Ä≥E is on the grounds of the emperor's palace in Tokyo.
The network of meridians and parallels is called the¬†graticule. Usually a globe will have a 10¬į or 15¬į graticule resolution, which means it shows meridians and parallels every 10¬į or 15¬į. Maps have widely varying graticule resolutions depending on their use and on the size of the area they are covering. Usually the meridians and parallels have the same resolution, but not always.
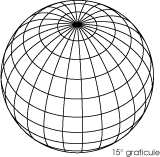
 The earth is very nearly a sphere 10,002 km (6215 mi) from equator to pole.[2] The typical globe is only about 0.00024 km (0.00015 mi) from equator to pole, which is economically sound, but there is a bit of a size difference. The ratio of the two sizes is called the scale of the globe, which in this case is 0.00024: 10,002 or 1:41,675,000 ‚ÄĒ in other words, the earth's circumference is 42 million times that of a 12-inch globe.
The earth is very nearly a sphere 10,002 km (6215 mi) from equator to pole.[2] The typical globe is only about 0.00024 km (0.00015 mi) from equator to pole, which is economically sound, but there is a bit of a size difference. The ratio of the two sizes is called the scale of the globe, which in this case is 0.00024: 10,002 or 1:41,675,000 ‚ÄĒ in other words, the earth's circumference is 42 million times that of a 12-inch globe.
 

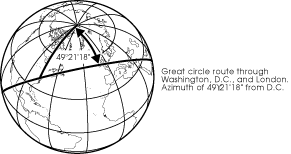
If the earth were flat then the shortest distance between two points would be a straight line, but since there is no such thing as a straight line on a sphere then something else must show the shortest distance. That something is a great circle, and if it is drawn completely then it goes all the way around the earth to the antipode, or point on the opposite side, and back to the starting point. The center of a great circle is the center of the earth, and great circles may be thought of as paths on the surface of the earth where planes cut through the center of it. All meridians are great circles, but no parallels are except the equator. A great circle going in a particular direction as seen from some point is called an azimuth (muth, not myooth), and usually its direction is measured as a number of degrees clockwise from north.
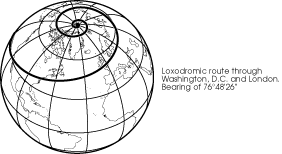
Mariners who have only a compass to help them prefer to travel paths whose direction does not change: a course of constant bearing, called a rhumb line, or, mathematically, a loxodrome. A loxodrome crosses each meridian at the same angle. A loxodrome is a great circle only if it is the equator or a meridian; any other rhumb between two points is longer than the great circle route between the same two points.

It is also convenient to talk about small circles sometimes. These are circles made by slicing through the earth with a plane at any angle so that the plane does not actually go through the center of the earth. All of the parallels except the equator are small circles, but none of the meridians are. Because a small circle is a circle it shows all of the points on the surface of the globe that are the same distance from the center of the small circle.

Here we must address the problem of¬†direction. Direction means what you think it means in a local sense, but probably not in a global sense. The common perception of direction goes something like this: you determine which way is east, for example, by measuring 90¬į clockwise from north. Then, you point in that direction to another person who is due east of you. He points due east of himself to another person, and so on to form a chain all away around the world. You would probably say that everyone in the chain and every point between is east of you. This is actually false, and technically none of the people in the chain are east of you. Your chain has made a rhumb line, a loxodrome, which is an interesting and useful measure of direction, but it is not the official definition.
According to the official definition, east follows the great circle that crosses your meridian at a 90¬į angle: the eastern azimuth. At first, this azimuth will be very close to your chain, but if you live in the northern hemisphere you will find the azimuth gradually dipping south, reaching the equator and going below it until it reaches the¬†latitude of opposite sign: the latitude that is as far south as you are north. It continues circling the back side of the earth and eventually returns to you after crossing the equator again.
When a projection has properties based on direction, you must understand clearly that these directions refer to the official meaning based on azimuths. Therefore, the retroazimuthal projections ‚ÄĒ those that let you find the direction to a center point from any other, for example, may not give you what you think you want. If you need maps that show intuitive direction then you should use those that have loxodromic properties: Mercator and Loximuthal.
As mentioned earlier, the earth is very nearly a sphere ‚ÄĒ but not quite. In the language of mathematicians the earth's shape is very close to an¬†ellipsoid, which is an ellipse (oval) rotated in three dimensions. Ellipsoids that are nearly spheres are sometimes called¬†spheroids. Astronomers call a body shaped like the earth an¬†oblate spheroid, which is a specific kind of ellipsoid made by rotating an ellipse in three dimensions around its shorter axis. But the earth has irregularities that keep it from being a simple geometric solid. Its true shape, whatever that happens to be, is called the¬†geoid. Although a perfectly spherical globe is not quite accurate in representing the earth, when making globes the difference is too small to worry about since variations in manufacturing technique can be proportionally greater than the geoid's deviation from a sphere. However, accurate regional maps require the earth to be modeled on an ellipsoid.

The largest part of a globe that you can see at one time is a hemisphere, or half of it. Any half of the globe is a hemisphere but some of them are named. The northern hemisphere is all areas north of the equator and the southern hemisphere is all areas south of it. The eastern hemisphere and western hemisphere are not so rigorously defined. Normally the eastern hemisphere means a bit more than a hemisphere: all of Africa, Australia, and Eurasia, and the western hemisphere means North and South America.
 
Globes are the best representation of the earth because all distance, areas, and shapes are proportionally correct. Unfortunately globes of any size are rather inconvenient to tote about and store, and detailed images of even a large country would require globes larger than a room. Using portions of a globe would work but they still don't lie down flat and would be like trying to store large potato chips (potato crisps) of all different sizes in book form.
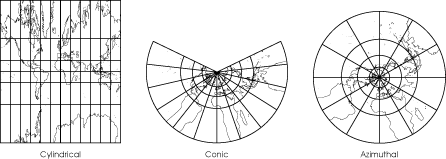
To deal with this problem ancient peoples created¬†maps. The earliest maps only showed very small portions of the earth and were very serviceable without worrying about spheres and such nonsense ‚ÄĒ indeed, they were not made as replacements for globes at all. But the Greeks had grander plans and by at latest 600¬†BC the idea arose of projecting the globe onto adevelopable surface.[3] This launched¬†cartography, the science of mapmaking. A developable surface is a surface that is capable of being unrolled onto a plane. Without allowing a surface having ripples, creases, or tears (all of which have critical drawbacks), a cylinder; a cone, and a plane (which was 2-dimensional to start with) are the only three objects that can be developed.

These three surfaces give rise to the three¬†natural projection classes that have members ‚ÄĒ¬†true projections ‚ÄĒ which can be displayed physically by projecting a light source through a transparent globe onto a developable surface used as a screen. The classes are called¬†cylindrical,¬†conic, and¬†azimuthal (because all azimuths from the center are straight lines and their directions are true).
Within the natural projection classes are many projections that cannot be projected physically, but rather are derived mathematically. They still fit within the three classes because they have similar appearances and obey certain critical mathematical rules. Any representation of the globe or part of the globe on a flat surface, such as a sheet of paper, can be called a projection.

Then there is a vast collection of projections that arise as modifications of the basic three groups or as purely mathematical entities. There have been many taxonomic systems devised to describe them. The pseudocylindrical group is universally accepted, being those projections with meridians curving toward the poles and straight, scale-invariant parallels (the scale of any given parallel is constant along its entire length). There are also references to pseudoazimuthal, polyconic,polycylindrical, pseudoconic, and others.

We describe here a class of mathematically derived projections that are both numerous and useful enough for their own designation: lenticular, or lens-shaped. These are projections whose meridians and parallels curve toward the poles and maintain or decrease their distances from each other going from the center of the map to the edges. Some writers herd some of these into the polyconic class and others into the pseudoazimuthal or miscellaneous classes, but this author has found their similarities to each other to be more useful than their lineage in describing their properties and has thus named and grouped them into a new class. One final miscellaneous class covers any that don't fit into the others.
In practice the distinction between true projections and mathematical projections is not so useful. Indeed, many true projections are cartographically useless while many mathematical projections are valuable, which is why they were developed. All projections can be described mathematically in the end.

Maps always show a distorted view of the earth because they are not curved in three dimensions. The cartographer (mapmaker) usually tries to make as accurate a map as possible, and that is why there are so many different projections: each projection distorts the earth in a different way and the cartographer tries to pick one that works best for the area being mapped.[4]
These distortions come in two principal varieties. Areal distortion causes different regions on the map to have disproportionate sizes with respect to each other. For example, many maps show Greenland to be larger than South America, when really it is less than 1/7th the size. Distortion of shape technically is called angular distortion, and it usually manifests itself as shearing, which means that map features are twisted or bent. Since globes have many properties and any of those properties can be destroyed by the projection, there are many other possible kinds of distortion. Some of these are scale distortion, which means that distances are not shown correctly with respect to each other; direction distortion, which means that directions are not shown correctly; and interruption, which means that two points next to each other on the globe are separated on the map.
Areal distortion and angular distortion can exist independently of each other, so a given projection might have only one of those two kinds of distortion. However all projections have scale distortion so it often is used as a convenient measure for the accuracy of a map. The amount of scale distortion is indirectly related to the amounts of angular and areal distortion. A map has a stated scale called the nominal scale or principal scale, which is somewhat arbitrary but usually equals the scale of the center of the map.[5] At any point of the map the scale may vary from the nominal scale, and the ratio of the two is called the scale factor at that point. Unless the projection has no angular distortion at the point being measured, the scale factor at that point will vary according to direction, and in that case the scale distortion could be defined in many different ways.
You should strive to be aware of scale distortion in maps. On maps that cover large areas of the globe you simply cannot measure the distance from any point on a map to another, multiply by the nominal scale, and expect to have obtained a correct distance. The measured distance on a map depends upon the real distance, the projection, the nominal scale of the map, the orientation of the globe before projecting, and the extent of the map. You can rely on measured distances only if the scale distortion along the path you measure is constant and if you happen to know what that constant is. There are special maps used for measuring distances from a specific point to any other point on the globe, so you should use them instead whenever possible.
A map's distortion can be conveniently shown by the Tissot indicatrix, drawn as a set of ovals at regular intervals on the graticule. The size of the ovals and their slants show you how much distortion the map has at the ovals' centers.
The map on the left below is¬†conformal, which means it has no angular distortion ‚ÄĒ any small area's shape is correct. But as you look toward the poles from the equator you see the circles becoming larger and larger, and in fact the poles cannot be shown because they are infinitely far from the equator. So a large area looks incorrect even though a small area does not because the different parts of the large area have the wrong sizes with respect to each other. On the other hand the map on the right has almost no correct shapes anywhere, but it has no areal distortion so it is called¬†equal-area. If you measure the area of any region of the globe and then measure the area of the projected region on an equal-area map that has the same scale as the globe, you will find the two areas to be exactly equal.
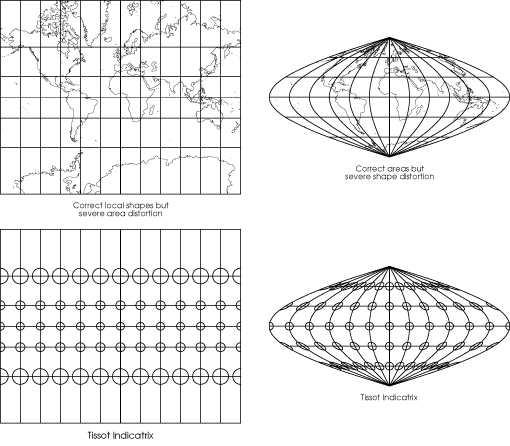
No map can be both conformal and equal-area, and many maps are neither. Conformality (the property of being conformal) is often important in surveyors' maps because conformal maps have no angular distortion and therefore local directions can be measured precisely from a given point once true north has been found at that point. In order to show land shapes correctly, conformality is also important in maps of areas that are large, but smaller than a hemisphere. Equivalence (the property of being equal-area) is very important in maps that approach or exceed a hemisphere in scope. At this size areal distortions in conformal maps become plainly visible and normally should be avoided. Equal-area maps will distort the shape, but conformal maps will distort large shapes also, and it is better to preserve sizes than to preserve neither shapes nor sizes.
It is always possible to choose a compromise projection that is neither equal-area nor conformal but that has some other desirable property. There are many other interesting properties: minimum error, which provides the least scale (or some other) distortion possible for the mapped area; azimuthal, which gives correct directions to all locations from the center;retroazimuthal, which gives correct direction to the center from all locations; equidistant, which gives correct distances to all locations from one or two points (or, another meaning which states that all meridians have correct scale); perspective, which provides a natural view of the earth from high altitude; loxodromic, which provides straight rhumb lines; gnomonic, providing straight great circles. Or perhaps a particular shape is interesting or more æsthetic than another. All of these are legitimate reasons for choosing a specific projection. Some projections can have more than one of these properties, but many properties are mutually exclusive in the same way that conformality and equivalence are.
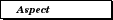
An¬†aspect must be chosen when projecting the globe. Simply speaking, the aspect is the position from which the earth is viewed when it is projected. Historically the aspects have been divided into¬†equatorial, or seen from the equator;¬†polar, or seen from one of the poles; or¬†oblique, which means seen from anywhere else. For example, in the middle map below the aspect is oblique, being centered at 45¬įN, 0¬įE. The aspect always corresponds to the point at the center of the map if the map is bilaterally symmetrical (the graticule is symmetrical about both the horizontal and vertical axes). In reality the idea of aspect is somewhat arbitrary because the polar aspect occurs at only two points, the equatorial aspect covers an entire great circle, and the oblique aspect covers everything except one great circle and two points. These unbalanced definitions made sense from a computational standpoint in times past: conics and cylindricals are easily computed in the equatorial aspect and azimuthals are simple in polar aspect. Computers obliterate the old reasons for doing things. From a modern standpoint any aspect is as feasible as any other.
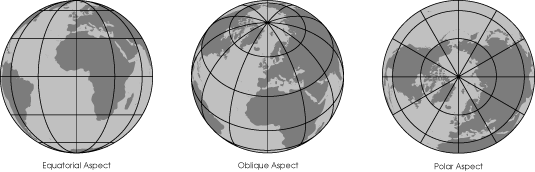
Sometimes it's convenient to think of the¬†projection center instead. The projection center is a numerically precise expression of aspect. The polar aspects have projection centers of 90¬įN or 90¬įS with any longitude. The equatorial aspect's projection center is 0¬įN with any longitude, and the oblique aspects have any other projection center. You may consider the polar and equatorial aspects to be special cases of the oblique aspect.
If a projection is a simple perspective, like the circular ones in this monologue, then its oblique aspect looks perfectly natural ‚ÄĒ just like what you see when you look at a globe. But almost all projections are mathematical, not perspective, and since the shapes of their graticules were made for the equatorial aspect they often look unusual when displayed in oblique and polar aspects (azimuthal projections look normal in polar as well). Of the following maps, the first is equatorial aspect, the last is polar, and the remainder are oblique.
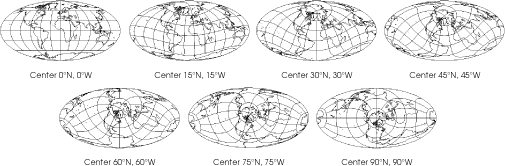

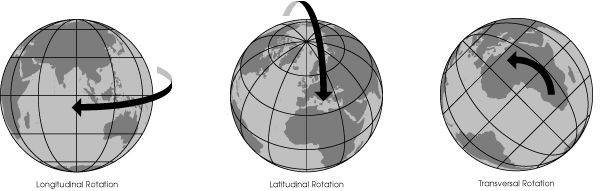
Besides changing the center of the projection, it is possible to rotate the globe around the projection center before projecting. This is called¬†transversal rotation. If the aspect is equatorial and the rotation is 90¬į then a¬†transverse projection results wherein the poles of the globe lie on the original equator of the projection. Of the following maps the first is a standard equatorial aspect and the last is a transverse projection.
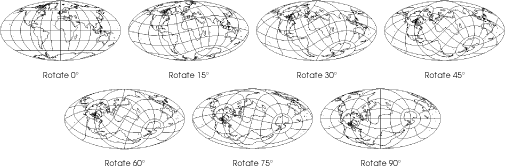
Most texts and mapping programs have you specify the coordinate on the original globe that you will be moving the north pole to when rotating the globe. Here we discuss a rotational angle instead.
To restate, you can rotate the globe three independent ways before projecting: longitudinal, where you merely spin the globe on its natural axis to bring a particular meridian to the projection center; latitudinal, where you bring a particular latitude to the projection center; and transversal, where you spin the earth around the axis formed by the projection center and the center of the globe.
1. The meridian you can see running through western Africa, western Europe, and England. The meridian was chosen in 1884 at the International Meridian Conference in Washington, D.C. It has no particular physical significance. 
2. In fact, the meter was originally defined to be 1/10,000,000th that distance, but the survey was off by 1,966 meters. It was a valiant effort. 
3. Yes, the Greeks knew the earth was a sphere, and they knew its exact size. In fact, so did medieval Europeans. The myth that people thought the earth is flat owes most of its life to fanciful American biographer Washington Irving and French Academy scholar Antoine-Jean Letronne, who propagated the idea to substantiate how enlightened society had become. The subject that Columbus tried to turn into an issue was the size of the earth, not the shape. Columbus was wrong, and the scholars knew it. [Russell] 
4. At least, that is the theory. Actually most maps have been created using the best projection that also happens to be easy to draw. Until recently cartographers could not use computers to help them, so for practicality's sake they were restricted to using tables of coordinates that had been computed laboriously for a few common projections applied to certain areas of the earth. 
5. Or, more precisely, the scale of the globe from which the map is being projected.


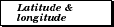


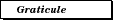

 The earth is very nearly a sphere 10,002 km (6215 mi) from equator to pole.[
The earth is very nearly a sphere 10,002 km (6215 mi) from equator to pole.[


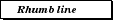














Comentaris publicats
Afegeix-hi un comentari: