Ley de Chapman-Kolmogórov
La ley de Chapman-Kolmogórov se basa en la ecuación del mismo nombre, a la que llegaron de forma independiente el matemático británico Sydney Chapman y el matemático ruso Andréi Kolmogórov. Enunciada de una forma sencilla dice: "la probabilidad de que dos hechos debidos al azar (y que cumplen unas condiciones determinadas), pasen conjuntamente... es "pequeñÃsima".
El concepto era conocido de antemano, y se empleaba en la investigación forense. Por ejemplo, se sabe que, en un incendio forestal, si hay un solo foco puede ser accidental, pero si hay dos la probabilidad de que sea provocado es altÃsima.
Dentro del entorno de entrada de datos de las máquinas de Bull1 (con tarjetas perforadas tipo Hollerith), se hacÃa una 2ª entrada de datos leyendo al mismo tiempo las tarjetas perforadas en la 1ª entrada, la máquina pitaba si habÃa alguna diferencia, en caso contrario se daba como correcta, ya que la probabilidad de error pasaba a ser "Ãnfima".
En ambos ejemplos se está aplicando la ley de Chapman-Kolmogórov, aunque no se explicite.
Ecuación de Chapman-Kolmogórov
En matemáticas, especÃficamente en teorÃa de probabilidad y, en particular, la teorÃa de procesos estocásticos Markovianos, la ecuación de Chapman-Kolmogórov es una identidad sobre las distribuciones de probabilidad conjunta de los diferentes conjuntos de coordenadas en un proceso estocástico.
Supongamos que { fi } es una colección indexada de variables aleatorias, es decir, un proceso estocástico. Hacemos
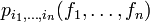
sea la función conjunta de densidad de probabilidad de los valores de las variables aleatorias de f1 a fn. Entonces, la ecuación de Chapman-Kolmogórov es
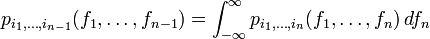
es decir, una marginalización directa sobre la variable estorbo
(Hay que tener en cuenta que todavÃa no hemos supuesto nada sobre el orden temporal (o cualquier otro) de las variables aleatorias, la ecuación anterior se aplica igualmente a la marginalización de cualquiera de ellos).
Cuando el proceso estocástico considerado es markoviano, la ecuación de Chapman-Kolmogóroves equivalente a una identidad en las densidades de transición. En la formación de la cadena de Márkov, se supone que i1 < ... < in. AsÃ, debido a la propiedad de Márkov
donde la probabilidad condicional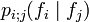 
es la probabilidad de transición entre los momentos 
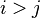. AsÃ, la ecuación de Chapman-Kolmogórov toma la forma
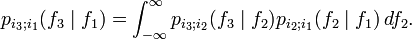
Cuando la distribución de probabilidad sobre el espacio de estados de una cadena de Márkov es discreta y la cadena de Márkov es homogénea, las ecuaciones de Chapman-Kolmogórov se pueden expresar en términos de multiplicación de matrices (que pueden ser de dimensión infinita), asÃ:
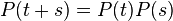
donde P(t) es la matriz de transición, es decir, si Xt es el estado del proceso en el momento t, entonces para dos estados cualesquiera i & j, tenemos
Referencias
- El legado de Andréi Nikoláevich Kolmogórov CurrÃculum Vitae y biografÃa. Escuela Kolmogórov. Ph.D. estudiantes y descendientes de A.N. Kolmogórov. A.N. Kolmogórovobras, libros, documentos, artÃculos. FotografÃas y retratos de A.N. Kolmogórov.
Comentaris publicats
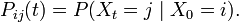
Afegeix-hi un comentari: